
 如图,某货轮在A处看灯塔B在货轮的北偏东75°,距离为12nmile,在A处看灯塔C在货轮的北偏西30°,距离为8nmile,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求:
如图,某货轮在A处看灯塔B在货轮的北偏东75°,距离为12nmile,在A处看灯塔C在货轮的北偏西30°,距离为8nmile,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求:分析 (1)在△ABD中使用正弦定理解出;
(2)在△ACD中使用余弦定理解出.
解答 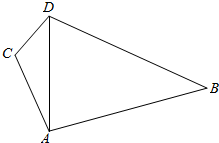 解:(1)在△ABD中,AB=12,∠ADB=60°,∠BAD=75°,∴B=45°,
解:(1)在△ABD中,AB=12,∠ADB=60°,∠BAD=75°,∴B=45°,
由正弦定理得$\frac{AB}{sin∠ADB}=\frac{AD}{sinB}$
∴AD=$\frac{AB•sin45°}{sin60°}$=4$\sqrt{6}$,∴A处与D处的距离为4$\sqrt{6}$nmile.
(2)在△ADC中,AC=8,AD=4$\sqrt{6}$,∠CAD=30°,
∴CD2=AD2+AC2-2AD•AC•cos30°.解得CD=$\sqrt{160-96\sqrt{2}}$=4$\sqrt{10-6\sqrt{2}}$.
∴灯塔C与D处的距离为4$\sqrt{10-6\sqrt{2}}$nmile.
点评 本题考查了解三角形的应用,构造合适的三角形是关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2] | B. | (-∞,2] | C. | [-2,+∞) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若|z1|=|z2|,则${z_1}^2={z_2}^2$ | B. | 若${z_1}=\overline{z_2}$,则$\overline{z_1}={z_2}$ | ||
| C. | 若|z1|=|z2|,则${z_1}•\overline{z_1}={z_2}•\overline{z_2}$ | D. | 若|z1-z2|=0,则$\overline{z_1}=\overline{z_2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f({0.7^6})<f({log_{0.7}}6)<f({6^{0.5}})$ | B. | f(0.76)<f(60.5)<f(log0.76) | ||
| C. | $f({log_{0.7}}6)<f({0.7^6})<f({6^{0.5}})$ | D. | $f({log_{0.7}}6)<f({6^{0.5}})<f({0.7^6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
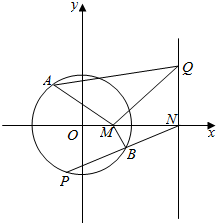 如图,自点M(1,0)引直线交椭圆$\frac{{x}^{2}}{4}$+y2=1于A,B两点,直线l:x=4与x轴交于点N,设点A关于x轴的对称点为P(异于点B).
如图,自点M(1,0)引直线交椭圆$\frac{{x}^{2}}{4}$+y2=1于A,B两点,直线l:x=4与x轴交于点N,设点A关于x轴的对称点为P(异于点B).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com