
分析 利用函数的奇偶性,单调性,即可判断,从而求出值域.
解答 解:函数的定义域是(-∞,0)∪(0,+∞),…(2分)
因为$f(-x)=\frac{{{2^x}+{2^{-x}}}}{{{2^{-x}}-{2^x}}}=-f(x)$,所以函数是奇函数. …(4分)
$f(x)=\frac{{{2^x}+{2^{-x}}}}{{{2^x}-{2^{-x}}}}=1+\frac{2}{{{2^{2x}}-1}}$,
设x1<x2,则$f({x_2})-f({x_1})=\frac{{2({2^{2{x_1}}}-{2^{2{x_2}}})}}{{({2^{2{x_1}}}-1)({2^{2{x_2}}}-1)}}$
当0<x1<x2时,$1<{2^{2{x_1}}}<{2^{2{x_2}}}$,所以f(x2)<f(x1),
所以在(0,+∞)上是减函数;…(8分)
当x1<x2<0时,${2^{2{x_1}}}<{2^{2{x_2}}}<1$,所以f(x2)<f(x1),
所以在(-∞,0)上也是减函数.
由$y=1+\frac{2}{{{2^{2x}}-1}}$,${2^x}=\frac{y+1}{y-1}$,所以y>1或y<-1…(12分)
点评 本题考查函数的奇偶性,单调性,值域,考查学生分析解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2] | B. | (-∞,2] | C. | [-2,+∞) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若|z1|=|z2|,则${z_1}^2={z_2}^2$ | B. | 若${z_1}=\overline{z_2}$,则$\overline{z_1}={z_2}$ | ||
| C. | 若|z1|=|z2|,则${z_1}•\overline{z_1}={z_2}•\overline{z_2}$ | D. | 若|z1-z2|=0,则$\overline{z_1}=\overline{z_2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f({0.7^6})<f({log_{0.7}}6)<f({6^{0.5}})$ | B. | f(0.76)<f(60.5)<f(log0.76) | ||
| C. | $f({log_{0.7}}6)<f({0.7^6})<f({6^{0.5}})$ | D. | $f({log_{0.7}}6)<f({6^{0.5}})<f({0.7^6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
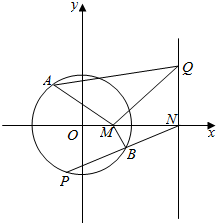 如图,自点M(1,0)引直线交椭圆$\frac{{x}^{2}}{4}$+y2=1于A,B两点,直线l:x=4与x轴交于点N,设点A关于x轴的对称点为P(异于点B).
如图,自点M(1,0)引直线交椭圆$\frac{{x}^{2}}{4}$+y2=1于A,B两点,直线l:x=4与x轴交于点N,设点A关于x轴的对称点为P(异于点B).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com