
已知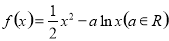 ,
,
(1)求函数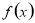 的单调区间;
的单调区间;
(2)求证:当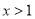 时,
时,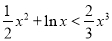 .
.
(1)当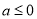 ,函数
,函数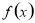 的单调区间为
的单调区间为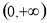 ,当
,当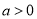 ,函数的
,函数的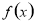 的单调增区间
的单调增区间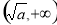 ,减区间
,减区间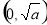 ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)函数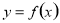 在某个区间内可导,则若
在某个区间内可导,则若 ,则
,则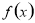 在这个区间内单调递增,若
在这个区间内单调递增,若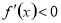 ,则
,则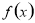 在这个区间内单调递减;(2)若可导函数
在这个区间内单调递减;(2)若可导函数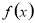 在指定的区间
在指定的区间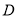 上单调递增(减),求参数问题,可转化为
上单调递增(减),求参数问题,可转化为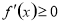
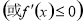 恒成立,从而构建不等式,要注意“=”是否可以取到.(3)对于恒成立的问题,常用到两个结论:(1)
恒成立,从而构建不等式,要注意“=”是否可以取到.(3)对于恒成立的问题,常用到两个结论:(1)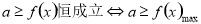 (2)
(2)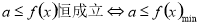 .
.
试题解析:【解析】
(1)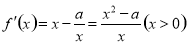
若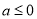 时,
时,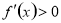 恒成立
恒成立
 函数
函数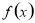 的单调区间为
的单调区间为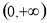
若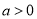 时,令
时,令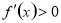 ,得
,得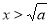 ;
;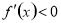 ,
,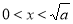
 函数的
函数的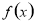 的单调增区间
的单调增区间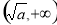 ,减区间
,减区间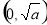
证明:设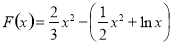
故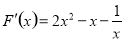
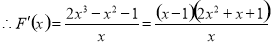
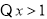 ,
,
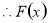 在
在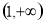 上为增函数.
上为增函数.
又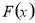 在
在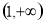 上连续,
上连续,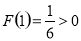 ,
,
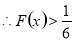 在(1,+∞)上恒成立.
在(1,+∞)上恒成立.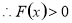 .
.
所以当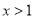 时,
时,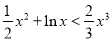 .
.
考点:(1)利用导数求函数的单调区间;(2)利用导数证明恒成立的问题.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破六 高考概率与统计(解析版) 题型:选择题
若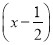 n的展开式中第3项的二项式系数是15,则展开式中所有项系数之和为( )
n的展开式中第3项的二项式系数是15,则展开式中所有项系数之和为( )
A.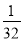 B.
B.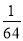 C.-
C.-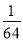 D.
D.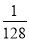
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破一 高考函数与导数(解析版) 题型:解答题
设函数f(x)=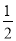 x2+2x+kln x,其中k≠0.
x2+2x+kln x,其中k≠0.
(1)当k>0时,判断f(x)在(0,+∞)上的单调性;
(2)讨论f(x)的极值点.
查看答案和解析>>
科目:高中数学 来源:2015届陕西省西安市高二下学期期末考试理科数学试卷(解析版) 题型:填空题
把一枚硬币任意抛掷三次,事件A=“至少一次出现反面”,事件B=“恰有一次出现正面”,则P(B|A)=________.
查看答案和解析>>
科目:高中数学 来源:2015届陕西省宝鸡市金台区高二下学期期末考试理科数学试卷(解析版) 题型:选择题
教育部直属师范大学免费师范毕业生一般回生源所在省份中小学校任教. 今年春节后,我校迎来了陕西师范大学数学系5名实习教师,若将5名实习教师分配到高一年级的3个班实习,每班至少1名,最多2名,则不同的分配方案有( )
A.60种 B.90种 C.120种 D.180种
查看答案和解析>>
科目:高中数学 来源:2015届陕西省高二上学期第一次月考理科数学试卷(解析版) 题型:选择题
一个等比数列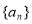 的前n项和为48,前2n项和为60,则前3n项和为( )
的前n项和为48,前2n项和为60,则前3n项和为( )
A.63 B.108 C.75 D.83
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com