Question

4．已知函数f（x）=4sin$\frac{ω}{2}xcos（{\frac{ω}{2}x-\frac{π}{3}}）-\sqrt{3}$（ω＞0）．
（Ⅰ）若ω=3，求f（x）在区间$[{\frac{5π}{9}，\frac{8π}{9}}]$上的最小值；
（Ⅱ）若函数f（x）的图象如图所示，求ω的值．

Answer 1

分析 （1）利用二倍角和两角和与差以及辅助角公式基本公式将函数化为y=Asin（ωx+φ）的形式，ω=3，求出f（x）解析式，x∈$[{\frac{5π}{9}，\frac{8π}{9}}]$上时，求出内层函数的取值范围，结合三角函数的图象和性质，求出f（x）的最小值，
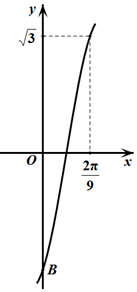
（2）图象过（$\frac{2π}{9}$，$\sqrt{3}$）带入即可求出ω的值．

解答 解：函数f（x）=4sin$\frac{ω}{2}xcos（{\frac{ω}{2}x-\frac{π}{3}}）-\sqrt{3}$（ω＞0）．
化解可得：f（x）=4sin$\frac{ω}{2}$x（$\frac{1}{2}cos\frac{ω}{2}x+\frac{\sqrt{3}}{2}sin\frac{ω}{2}x$）$-\sqrt{3}$
=2sin$\frac{ω}{2}$xcos$\frac{ωx}{2}$+2$\sqrt{3}$sin²$\frac{ωx}{2}$$-\sqrt{3}$
═sinωx+$\sqrt{3}$（1-cosωx）$-\sqrt{3}$
=sinωx-$\sqrt{3}$cosωx
=2sin（$ωx-\frac{π}{3}$）
（I）∵ω=3，
∴$f（x）=2sin（{3x-\frac{π}{3}}）$．
∵$\frac{5π}{9}≤x≤\frac{8π}{9}$，
∴$\frac{4π}{3}≤3x-\frac{π}{3}≤\frac{7π}{3}$．
所以，当$3x-\frac{π}{3}=\frac{3π}{2}$，即$x=\frac{11π}{18}$时，函数f（x）的最小值为-2．
（II）图象过（$\frac{2π}{9}$，$\sqrt{3}$）
即$f（\frac{2π}{9}）=\sqrt{3}$，
故而$sin（{\frac{2π}{9}ω-\frac{π}{3}}）=\frac{{\sqrt{3}}}{2}$
$\frac{2π}{9}ω-\frac{π}{3}=2kπ+\frac{π}{3}或2kπ+\frac{2π}{3}，k∈{Z}则ω=3+9k或\frac{9}{2}+9k，k∈Z$．
又由图象可知，$\frac{2π}{9}＜\frac{T}{2}$，即$T＞\frac{4π}{9}$，
所以$ω＜\frac{9}{2}$
又因为ω＞0，所以ω=3．

点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用，利用三角函数公式将函数进行化简是解决本题的关键．属于中档题．