
| A. | {-4,6} | B. | $\left\{{-\frac{7}{4},6}\right\}$ | C. | $\left\{{-4,-\frac{7}{4}}\right\}$ | D. | $\left\{{-4,-\frac{7}{4},6}\right\}$ |
分析 画出满足约束条件的可行域,求出目标函数的最大值,从而建立关于m的等式,即可得出答案.
解答 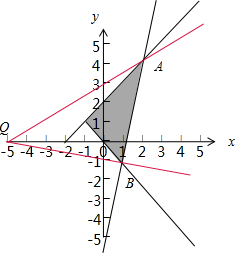 解:由z=x+my得y=-$\frac{1}{m}$x+$\frac{z}{m}$,
解:由z=x+my得y=-$\frac{1}{m}$x+$\frac{z}{m}$,
作出不等式组对应的平面区域如图:
∵z=x+my的最小值为-5,
∴此时z=x+my=-5,
此时目标函数过定点Q(-5,0),
作出x+my=-5的图象,
由图象知当m>0时,直线z=x+my,
经过B时,取得最小值-5.
当m<0时,由平移可知当直线y=-$\frac{1}{m}$x+$\frac{z}{m}$,
经过点A时,目标函数取得最小值-5,此时满足条件,
由$\left\{\begin{array}{l}{x-y+2=0}\\{5x-y-6=0}\end{array}\right.$,解得A(2,4),
同时,A也在直线x+my=-5上,
代入得2+4m=-5,解得m=-$\frac{7}{4}$,
由$\left\{\begin{array}{l}{5x-y-6=0}\\{x=y}\end{array}\right.$解得B(1,-1)
同时,B也在直线x+my=-5上,
代入得1-m=-5,解得m=6,
则实数m取值集合是:{-$\frac{7}{4}$,6}.
故选:B.
点评 本题主要考查线性规划的应用,根据目标函数的几何意义确定取得最小值的最优解是解决本题的关键.


科目:高中数学 来源: 题型:解答题
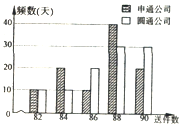 几年来,网上购物风靡,快递业迅猛发展,某市的快递业务主要由两家快递公司承接,即圆通公司与申通公司:“快递员”的工资是“底薪+送件提成”:这两家公司对“快递员”的日工资方案为:圆通公司规定快递员每天底薪为70元,每送件一次提成1元;申通公司规定快递员每天底薪为120元,每日前83件没有提成,超过83件部分每件提成10元,假设同一公司的快递员每天送件数相同,现从这两家公司各随机抽取一名快递员并记录其100天的送件数,得到如下条形图:
几年来,网上购物风靡,快递业迅猛发展,某市的快递业务主要由两家快递公司承接,即圆通公司与申通公司:“快递员”的工资是“底薪+送件提成”:这两家公司对“快递员”的日工资方案为:圆通公司规定快递员每天底薪为70元,每送件一次提成1元;申通公司规定快递员每天底薪为120元,每日前83件没有提成,超过83件部分每件提成10元,假设同一公司的快递员每天送件数相同,现从这两家公司各随机抽取一名快递员并记录其100天的送件数,得到如下条形图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
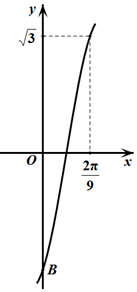 已知函数f(x)=4sin$\frac{ω}{2}xcos({\frac{ω}{2}x-\frac{π}{3}})-\sqrt{3}$(ω>0).
已知函数f(x)=4sin$\frac{ω}{2}xcos({\frac{ω}{2}x-\frac{π}{3}})-\sqrt{3}$(ω>0).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
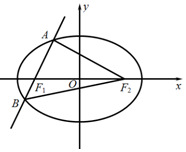 如图,已知F1、F2是椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,直线l:y=k(x+1)经过左焦点F1,且与椭圆G交于A、B两点,△ABF2的周长为$4\sqrt{3}$.
如图,已知F1、F2是椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,直线l:y=k(x+1)经过左焦点F1,且与椭圆G交于A、B两点,△ABF2的周长为$4\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{3\sqrt{5}}{2}$ | C. | 2$\sqrt{2}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com