
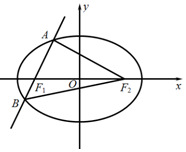
 如图,已知F1、F2是椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,直线l:y=k(x+1)经过左焦点F1,且与椭圆G交于A、B两点,△ABF2的周长为$4\sqrt{3}$.
如图,已知F1、F2是椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,直线l:y=k(x+1)经过左焦点F1,且与椭圆G交于A、B两点,△ABF2的周长为$4\sqrt{3}$.分析 (Ⅰ)由题意可知:c=1,4a=4$\sqrt{3}$,b2=a2-c2=3-1=2.即可求得椭圆方程;
(Ⅱ)分类讨论,假设|AF2|=|BF2|,利用作差法,即可求得x1+x2=6.(与x1≤$\sqrt{3}$,x2≤$\sqrt{3}$,x1+x2≤2$\sqrt{3}$<6,矛盾),将直线方程代入椭圆方程由韦达定理:${x_1}+{x_2}=-\frac{{6{k^2}}}{{3{k^2}+2}}$=6,矛盾.故|AF2|≠|BF2|.再证明AB不可能为等腰直角三角形的直角腰.由勾股定理得:${m^2}+{(2\sqrt{3}-m)^2}=4$,此方程无解.故不存在这样的等腰直角三角形.
解答 解:(Ⅰ)设椭圆G的半焦距为c,因为直线l与x轴的交点为(-1,0),故c=1.
又△ABF2的周长为$4\sqrt{3}$,即$|{AB}|+|{A{F_2}}|+|{B{F_2}}|=4a=4\sqrt{3}$,故a=$\sqrt{3}$.
所以,b2=a2-c2=3-1=2.
因此,椭圆G的标准方程为$\frac{x^2}{3}+\frac{y^2}{2}=1$;
注:本小题也可以用焦点和离心率作为条件,即将周长换离心率.
(Ⅱ)不存在.理由如下:先用反证法证明AB不可能为底边,即|AF2|≠|BF2|.
由题意知F2(1,0),设A(x1,y1),B(x2,y2),假设|AF2|=|BF2|,
则$\sqrt{{{({x_1}-1)}^2}+y_1^2}=\sqrt{{{({x_2}-1)}^2}+y_2^2}$,
又$\frac{x_1^2}{3}+\frac{y_1^2}{2}=1$,$\frac{x_2^2}{3}+\frac{y_2^2}{2}=1$,代入上式,消去$y_1^2,y_2^2$,得:(x1-x2)(x1+x2-6)=0.
因为直线l斜率存在,所以直线l不垂直于x轴,所以x1≠x2,故x1+x2=6(与x1≤$\sqrt{3}$,x2≤$\sqrt{3}$,x1+x2≤2$\sqrt{3}$<6,矛盾).
联立方程$\left\{\begin{array}{l}\frac{x^2}{3}+\frac{y^2}{2}=1\\ y=k(x+1)\end{array}\right.$,得:(3k2+2)x2+6k2x+3k2-6=0,
所以${x_1}+{x_2}=-\frac{{6{k^2}}}{{3{k^2}+2}}$=6,矛盾.
故|AF2|≠|BF2|.
再证明AB不可能为等腰直角三角形的直角腰.
假设△ABF2为等腰直角三角形,不妨设A为直角顶点.
设|AF1|=m,则$|{A{F_2}}|=2\sqrt{3}-m$,
在△AF1F2中,由勾股定理得:${m^2}+{(2\sqrt{3}-m)^2}=4$,此方程无解.
故不存在这样的等腰直角三角形.
注:本题也可改为是否存在直角三角形?会简单一些.改为是否存在等腰三角形则不易计算,也可修改椭圆方程使存在等腰直角三角形.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,两点之间的距离公式,考查计算能力,分类讨论思想,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2$\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-4,6} | B. | $\left\{{-\frac{7}{4},6}\right\}$ | C. | $\left\{{-4,-\frac{7}{4}}\right\}$ | D. | $\left\{{-4,-\frac{7}{4},6}\right\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{π}{6}$,$\frac{π}{6}$) | B. | (kπ-$\frac{π}{6}$,kπ+$\frac{π}{6}$)(k∈π) | ||
| C. | (2kπ-$\frac{π}{6}$,2kπ+$\frac{π}{6}$)(k∈Z) | D. | R |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错导致结论错 | B. | 小前提错导致结论错 | ||
| C. | 推理形式错导致结论错 | D. | 大前提和小前提错导致结论错 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com