练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．与复数z的实部相等，虚部互为相反数的复数叫做z的共轭复数，并记作$\overline z$，若z=i（3-2i）（其中i为复数单位），则$\overline z$=（　　）
    A．3-2iB．3+2iC．2+3iD．2-3i

    分析 利用复数代数形式的乘除运算化简z得答案．

    解答 解：由z=i（3-2i）=2+3i，
    得$\overline{z}=2-3i$．
    故选：D．

    点评 本题考查了复数代数形式的乘除运算，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．设正实数x，y，z满足x2-3xy+4y2-z=0，则当$\frac{z}{xy}$取得最小值时，x+2y-z的最大值为（　　）
    A．1B．$\frac{9}{8}$C．2D．$\frac{9}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知集合A={x|0＜4-x＜2}，B={x|3x-1≤9}，则A∩B=（　　）
    A．（2，3）B．（2，4）C．（2，3]D．[2，3]

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．若正实数x，y满足x2+2xy-1=0，则2x+y的最小值为$\sqrt{3}$ ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知函数f（x）=$\left\{\begin{array}{l}{\frac{1}{4}x+1，x≤1}\\{lnx，x＞1}\end{array}\right.$，则方程f（x）=ax恰有两个不同的实数根时，实数a的取值范围是（　　）
    A．（0，$\frac{1}{e}$）B．[$\frac{1}{4}$，$\frac{1}{e}$）C．（0，$\frac{1}{4}$]D．（$\frac{1}{4}$，e）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

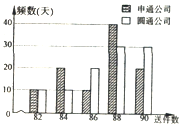    20．几年来，网上购物风靡，快递业迅猛发展，某市的快递业务主要由两家快递公司承接，即圆通公司与申通公司：“快递员”的工资是“底薪+送件提成”：这两家公司对“快递员”的日工资方案为：圆通公司规定快递员每天底薪为70元，每送件一次提成1元；申通公司规定快递员每天底薪为120元，每日前83件没有提成，超过83件部分每件提成10元，假设同一公司的快递员每天送件数相同，现从这两家公司各随机抽取一名快递员并记录其100天的送件数，得到如下条形图：
    （1）求申通公司的快递员一日工资y（单位：元）与送件数n的函数关系；
    （2）若将频率视为概率，回答下列问题：
    ①记圆通公司的“快递员”日工资为X（单位：元），求X的分布列和数学期望；
    ②小王想到这两家公司中的一家应聘“快递员”的工作，如果仅从日收入的角度考虑，请你利用所学过的统计学知识为他作出选择，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．下列各区间中，是函数f（x）=2cos2x的一个单调递增区间的为（　　）
    A．（0，$\frac{π}{2}$）B．（$\frac{π}{2}$，π）C．（-$\frac{π}{4}$，$\frac{π}{4}$）D．（$\frac{π}{4}$，$\frac{3π}{4}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

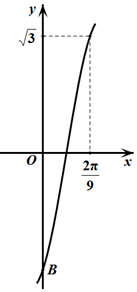    4．已知函数f（x）=4sin$\frac{ω}{2}xcos（{\frac{ω}{2}x-\frac{π}{3}}）-\sqrt{3}$（ω＞0）．
    （Ⅰ）若ω=3，求f（x）在区间$[{\frac{5π}{9}，\frac{8π}{9}}]$上的最小值；
    （Ⅱ）若函数f（x）的图象如图所示，求ω的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．若$\frac{ai}{2-i}$=$\frac{1-2i}{5}$（i为虚数单位），则实数a的值为（　　）
    A．1B．-1C．±1D．2

    查看答案和解析>>

    同步练习册答案