
分析 利用方程的根与系数之间的关系进行转化列出关于k的不等式,通过求解不等式确定出k的取值范围,注意进行等价转化.
解答 解:方程( k-2 )x2-( 3k+6 )x+6k=0有两个负根?$\left\{\begin{array}{l}{\frac{3k+6}{k-2}<0}\\{\frac{6k}{k-2}>0}\\{(3k+6)^{2}-24k(k-2)≥0}\end{array}\right.$,
因此得出k的取值范围是$[{-\frac{2}{5},0})$.
故答案为$[{-\frac{2}{5},0})$.
点评 本题考查一元二次方程方程根与系数的关系,考查韦达定理的应用,关键要列出关于字母k的取值范围,通过求解不等式组确定出所求的取值范围.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
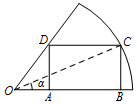 为了废物利用,准备把半径为2,圆心角为$\frac{π}{3}$的扇形铁片余料剪成如图所示的内接矩形ABCD.试用图中α表出内接矩形ABCD的面积S.
为了废物利用,准备把半径为2,圆心角为$\frac{π}{3}$的扇形铁片余料剪成如图所示的内接矩形ABCD.试用图中α表出内接矩形ABCD的面积S.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A⊆B | B. | A∪B=A | C. | A∩B=∅ | D. | A∩∁RB≠∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
| 年龄低于45岁的人数 | 年龄不低于45岁的人数 | 合计 | |
| 不赞成 | 3 | 10 | 13 |
| 赞成 | 27 | 10 | 37 |
| 合计 | 30 | 20 | 50 |
| P(X2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com