
°æƒø°øƒ≥…Á«¯Œ™¡ÀΩ‚æ”√Ò≤Œº”Ô˝∂Õ¡∂«Èøˆ£¨Àʪ˙≥È»°18√˚ƒ––‘æ”√Ò£¨12√˚≈Æ–‘æ”√Ò∂‘À˚√«≤Œº”Ô˝∂Õ¡∂µƒ«ÈøˆΩ¯––Œ æ̵˜≤ȣƜ÷∞¥≤Œº”Ô˝∂Õ¡∂µƒ«ÈøˆΩ´æ”√Ò∑÷≥…3¿ý£∫º◊¿ý(≤ª≤Œº”Ô˝∂Õ¡∂)£¨““¿ý(≤Œº”Ô˝∂Õ¡∂£¨µ´∆Ωæ˘√ø÷Ð≤Œº”Ô˝∂Õ¡∂µƒ ±º‰≤ª≥¨π˝5∏ˆ–° ±)£¨±˚¿ý(≤Œº”Ô˝∂Õ¡∂£¨«“∆Ωæ˘√ø÷Ð≤Œº”Ô˝∂Õ¡∂µƒ ±º‰≥¨π˝5∏ˆ–° ±)£¨µ˜≤ÈΩ·π˚»Áœ¬±Ì£∫
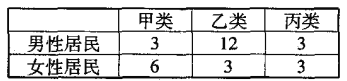
(1)∏˘æð±Ì÷–µƒÕ≥º∆ ˝æð£¨ÕÍ≥…œ¬√Ê¡–¡™±Ì£¨≤¢≈–∂œ «∑Ò”–![]() µƒ∞—Œ’»œŒ™≤Œº”Ô˝∂Õ¡∂”Î∑ҔΖ‘±”–πÿ?
µƒ∞—Œ’»œŒ™≤Œº”Ô˝∂Õ¡∂”Î∑ҔΖ‘±”–πÿ?
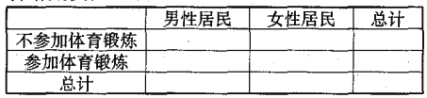
(2)¥”≥È≥ˆµƒ≈Æ–‘æ”√Ò÷–‘ŸÀʪ˙≥È»°2»ÀΩ¯“ª≤Ω¡ÀΩ‚«Èøˆ£¨«ÛÀ˘≥È»°µƒ2»À÷–““¿ý£¨±˚¿ý∏˜”–1»Àµƒ∏≈¬ £Æ
∏Ω£∫![]()
|
|
|
|
|
|
|
|
|
|
°æ¥∞∏°ø(1) ”–£ª(2)![]() .
.
°æΩ‚Œˆ°ø
£®1£©∏˘æð±Ì÷– ˝æðÃÓ–¥¡–¡™±Ì£¨º∆À„π€≤‚÷µ£¨∂‘’’¡ŸΩÁ÷µµ√≥ˆΩ·¬€£ª
£®2£©”√¡–æŸ∑®º∆À„ª˘±æ ¬º˛ ˝£¨¿˚”√π≈µ‰∏≈–Õπ´ Ωº¥ø…«Û≥ˆ∂‘”¶µƒ∏≈¬ ÷µ.
£®1£©
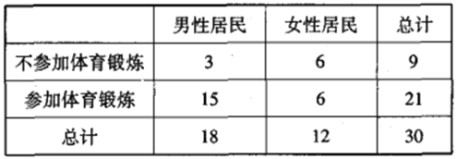
![]() £¨
£¨
°ý”–90%µƒ∞—Œ’»œŒ™≤Œº”Ô˝∂Õ¡∂”Î∑ҔΖ‘±”–πÿ£ª
£®2£©º«»˝√˚““¿ý≈Æ–‘æ”√ÒŒ™![]() £¨
£¨![]() £¨
£¨![]() £¨»˝√˚±˚¿ý≈Æ–‘æ”√ÒŒ™
£¨»˝√˚±˚¿ý≈Æ–‘æ”√ÒŒ™![]() £¨
£¨![]() £¨
£¨![]() £¨¥”≥È≥ˆµƒ““¿ý°¢
£¨¥”≥È≥ˆµƒ““¿ý°¢
±˚¿ý≈Æ–‘æ”√Ò÷–Àʪ˙≥È»°2»Àµƒª˘±æ ¬º˛Œ™£∫![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
![]() £¨
£¨![]() £¨π≤º∆15∏ˆ£¨
£¨π≤º∆15∏ˆ£¨
≥È≥ˆµƒ¡Ω»À÷–““¿ý£¨±˚¿ý∏˜”–1»À∞¸∫¨µƒª˘±æ ¬º˛Œ™£∫![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨π≤º∆9∏ˆ£¨
£¨π≤º∆9∏ˆ£¨
°ý≥È≥ˆµƒ¡Ω»À÷–““¿ý£¨±˚¿ý∏˜”–1»Àµƒ∏≈¬ Œ™£∫
![]() .
.



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄‘≤÷˘![]() ÷–£¨µ„
÷–£¨µ„![]() °¢
°¢![]() ∑÷±Œ™…œ°¢œ¬µ◊√ʵƒ‘≤–ƒ£¨∆Ω√Ê
∑÷±Œ™…œ°¢œ¬µ◊√ʵƒ‘≤–ƒ£¨∆Ω√Ê![]() «÷·Ωÿ√Ê£¨µ„
«÷·Ωÿ√Ê£¨µ„![]() ‘⁄…œµ◊√Ê‘≤÷Ð…œ£®“Ï”⁄
‘⁄…œµ◊√Ê‘≤÷Ð…œ£®“Ï”⁄![]() °¢
°¢![]() £©£¨µ„
£©£¨µ„![]() Œ™œ¬µ◊√Ê‘≤ª°
Œ™œ¬µ◊√Ê‘≤ª°![]() µƒ÷–µ„£¨µ„
µƒ÷–µ„£¨µ„![]() ”ε„
”ε„![]() ‘⁄∆Ω√Ê
‘⁄∆Ω√Ê![]() µƒÕ¨≤ý£¨‘≤÷˘
µƒÕ¨≤ý£¨‘≤÷˘![]() µƒµ◊√Ê∞Îæ∂Œ™1£¨∏þŒ™2.
µƒµ◊√Ê∞Îæ∂Œ™1£¨∏þŒ™2.
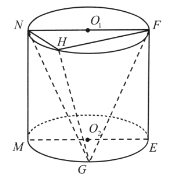
£®1£©»Ù∆Ω√Ê![]() ∆Ω√Ê
∆Ω√Ê![]() £¨÷§√˜£∫
£¨÷§√˜£∫![]() £ª
£ª
£®2£©»Ù÷±œþ![]() ”Î∆Ω√Ê
”Î∆Ω√Ê![]() À˘≥…œþ√ÊΩ«
À˘≥…œþ√ÊΩ«![]() µƒ’˝œ“÷µµ»”⁄
µƒ’˝œ“÷µµ»”⁄![]() £¨÷§√˜£∫∆Ω√Ê
£¨÷§√˜£∫∆Ω√Ê![]() ”Î∆Ω√Ê
”Î∆Ω√Ê![]() À˘≥…»Ò∂˛√ÊΩ«µƒ∆Ω√ÊΩ«¥Û”⁄
À˘≥…»Ò∂˛√ÊΩ«µƒ∆Ω√ÊΩ«¥Û”⁄![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕºÀ˘ 棨‘⁄»˝¿‚◊∂![]() ÷–£¨
÷–£¨![]() ”Î
”Î![]() ∂º «±þ≥§Œ™2µƒµ»±þ»˝Ω«–Œ£¨
∂º «±þ≥§Œ™2µƒµ»±þ»˝Ω«–Œ£¨![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() ∑÷± «¿‚
∑÷± «¿‚![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() µƒ÷–µ„.
µƒ÷–µ„.
£®1£©÷§√˜£∫Àƒ±þ–Œ![]() Œ™æÿ–Œ£ª
Œ™æÿ–Œ£ª
£®2£©»Ù∆Ω√Ê![]() ∆Ω√Ê
∆Ω√Ê![]() £¨«Ûµ„
£¨«Ûµ„![]() µΩ∆Ω√Ê
µΩ∆Ω√Ê![]() µƒæý¿Î.
µƒæý¿Î.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤![]() £∫
£∫![]() µƒ¿Î–ƒ¬ Œ™
µƒ¿Î–ƒ¬ Œ™![]() £¨÷±œþ
£¨÷±œþ![]() ±ª‘≤
±ª‘≤![]() Ωÿµ√µƒœ“≥§Œ™
Ωÿµ√µƒœ“≥§Œ™![]() .
.
£®1£©«ÛÕ÷‘≤![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©π˝µ„![]() µƒ÷±œþ
µƒ÷±œþ![]() ΩªÕ÷‘≤
ΩªÕ÷‘≤![]() ”⁄
”⁄![]() £¨
£¨![]() ¡Ωµ„£¨‘⁄
¡Ωµ„£¨‘⁄![]() ÷·…œ «∑ҥʑ⁄∂®µ„
÷·…œ «∑ҥʑ⁄∂®µ„![]() £¨ πµ√
£¨ πµ√![]() Œ™∂®÷µ£ø»Ù¥Ê‘⁄£¨«Û≥ˆµ„
Œ™∂®÷µ£ø»Ù¥Ê‘⁄£¨«Û≥ˆµ„![]() µƒ◊¯±Í∫Õ
µƒ◊¯±Í∫Õ![]() µƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
µƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤![]() µƒ”“∂•µ„Œ™
µƒ”“∂•µ„Œ™![]() £¨◊ÛΩπµ„Œ™
£¨◊ÛΩπµ„Œ™![]() £¨¿Î–ƒ¬
£¨¿Î–ƒ¬ ![]() £¨π˝µ„
£¨π˝µ„![]() µƒ÷±œþ”ÎÕ÷‘≤Ωª”⁄¡Ì“ª∏ˆµ„
µƒ÷±œþ”ÎÕ÷‘≤Ωª”⁄¡Ì“ª∏ˆµ„![]() £¨«“µ„
£¨«“µ„![]() ‘⁄
‘⁄![]() ÷·…œµƒ…‰”∞«°∫√Œ™µ„
÷·…œµƒ…‰”∞«°∫√Œ™µ„![]() £¨»Ù
£¨»Ù![]() £Æ
£Æ
(1)«ÛÕ÷‘≤![]() µƒ±Í◊º∑Ω≥ãª
µƒ±Í◊º∑Ω≥ãª
(2)π˝‘≤![]() …œ»Œ“‚“ªµ„
…œ»Œ“‚“ªµ„![]() ◊˜‘≤
◊˜‘≤![]() µƒ«–œþ
µƒ«–œþ![]() ”ÎÕ÷‘≤Ωª”⁄
”ÎÕ÷‘≤Ωª”⁄![]() £¨
£¨![]() ¡Ωµ„£¨“‘
¡Ωµ„£¨“‘![]() Œ™÷±æ∂µƒ‘≤ «∑Òπ˝∂®µ„£¨»Áπ˝∂®µ„£¨«Û≥ˆ∏√∂®µ„£ª»Ù≤ªπ˝∂®µ„£¨«ÎÀµ√˜¿Ì”…£Æ
Œ™÷±æ∂µƒ‘≤ «∑Òπ˝∂®µ„£¨»Áπ˝∂®µ„£¨«Û≥ˆ∏√∂®µ„£ª»Ù≤ªπ˝∂®µ„£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øÀ´«˙œþ![]()
![]() µƒ◊Û°¢”“Ωπµ„∑÷±Œ™
µƒ◊Û°¢”“Ωπµ„∑÷±Œ™![]() £¨π˝
£¨π˝![]() ◊˜«„–±Ω«Œ™
◊˜«„–±Ω«Œ™![]() µƒ÷±œþ”Î
µƒ÷±œþ”Î![]() ÷·∫ÕÀ´«˙œþµƒ”“÷ß∑÷±Ωª”⁄
÷·∫ÕÀ´«˙œþµƒ”“÷ß∑÷±Ωª”⁄![]() ¡Ωµ„£¨»Ùµ„
¡Ωµ„£¨»Ùµ„![]() ∆Ω∑÷œþ∂Œ
∆Ω∑÷œþ∂Œ![]() £¨‘Ú∏√À´«˙œþµƒ¿Î–ƒ¬ «£® £©
£¨‘Ú∏√À´«˙œþµƒ¿Î–ƒ¬ «£® £©
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
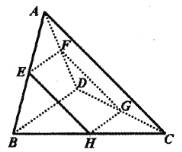
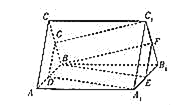
°æƒø°ø»ÁÕºÀ˘ 棨»˝¿‚÷˘ABC©ÅA1B1C1µƒ≤ý¿‚¥π÷±”⁄µ◊√Ê£¨«“µ◊√Ê «±þ≥§Œ™2µƒ’˝»˝Ω«–Œ£¨AA1£Ω3£¨µ„D£¨E£¨F£¨G∑÷± «À˘‘⁄¿‚µƒ÷–µ„£Æ
£®¢Ò£©÷§√˜£∫∆Ω√ÊBEF°Œ∆Ω√ÊDA1C1£ª
£®¢Ú£©«Û»˝¿‚÷˘ABC©ÅA1B1C1º–‘⁄∆Ω√ÊBEF∫Õ∆Ω√ÊDA1C1÷ƺ‰µƒ≤ø∑÷µƒÃª˝£Æ
∏Ω£∫îõƒÃª˝![]() £¨∆‰÷–S∫ÕS°‰∑÷± «…œ°¢œ¬µ◊√Ê√ʪ˝£¨h «Ã®Ãµƒ∏þ£Æ
£¨∆‰÷–S∫ÕS°‰∑÷± «…œ°¢œ¬µ◊√Ê√ʪ˝£¨h «Ã®Ãµƒ∏þ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
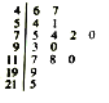
°æƒø°øø’∆¯÷ ¡ø÷∏ ˝£®Air Quality Index£¨ºÚ≥∆AQI£© «∂®¡ø√Ë ˆø’∆¯÷ ¡ø◊¥øˆµƒ÷∏ ˝£¨ø’∆¯÷ ¡ø∞¥’’AQI¥Û–°∑÷Œ™¡˘º∂£¨0°´50Œ™”≈£ª51°´100Œ™¡º£ª101°´150Œ™«·∂»Œ€»æ£ª151°´200Œ™÷–∂»Œ€»æ£ª201°´300Œ™÷ÿ∂»Œ€»æ£ª¥Û”⁄300Œ™—œ÷ÿŒ€»æ.ƒ≥ª∑±£»À ø¥”µ±µÿƒ≥ƒÍµƒAQIº«¬º ˝æð÷–£¨Àʪ˙≥È»°¡À15ÃϵƒAQI ˝æ𣨔√»ÁÕºÀ˘ 浃敓∂Õºº«¬º.∏˘æð∏√Õ≥º∆ ˝æð£¨π¿º∆¥Àµÿ∏√ƒÍø’∆¯÷ ¡øŒ™”≈ªÚ¡ºµƒÃÏ ˝‘ºŒ™__________£Æ£®∏√ƒÍŒ™366ÃÏ£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∆ªπ˚ «»À√«»’≥£…˙ªÓ÷–≥£º˚µƒ”™—¯–ÕÀÆπ˚.ƒ≥µÿÀÆπ˚≈˙∑¢ –≥°œ˙ €¿¥◊‘5∏ˆ≤ªÕ¨≤˙µÿµƒ∏ª ø∆ªπ˚£¨∏˜≤˙µÿµƒ∞¸◊∞πÊ∏ÒœýÕ¨,À¸√«µƒ≈˙∑¢º€∏Ò£®‘™/œ‰£©∫Õ –≥°∑ð∂Ó»Áœ¬£∫
≤˙µÿ |
|
|
|
|
|
≈˙∑¢º€∏Ò |
|
|
|
|
|
–≥°∑ð∂Ó |
|
|
|
|
|
–≥°∑ð∂Ó“ý≥∆°∞ –≥°’º”–¬ °±.÷∏ƒ≥“ª≤˙∆∑µƒœ˙ €¡ø‘⁄ –≥°Õ¨¿ý≤˙∆∑÷–À˘’º±»÷ÿ.
£®1£©¥”∏√µÿ≈˙∑¢ –≥°œ˙ €µƒ∏ª ø∆ªπ˚÷–Àʪ˙≥È»°“ªœ‰£¨«Û∏√œ‰∆ªπ˚º€∏ÒµÕ”⁄![]() ‘™µƒ∏≈¬ £ª
‘™µƒ∏≈¬ £ª
£®2£©∞¥ –≥°∑ð∂ÓΩ¯––∑÷≤„≥È—˘£¨Àʪ˙≥È»°![]() œ‰∏ª ø∆ªπ˚Ω¯––ºÏ—È£¨
œ‰∏ª ø∆ªπ˚Ω¯––ºÏ—È£¨
¢Ÿ¥”≤˙µÿ![]() π≤≥È»°
π≤≥È»°![]() œ‰,«Û
œ‰,«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
¢⁄¥”’‚![]() œ‰∆ªπ˚÷–Àʪ˙≥È»°¡Ωœ‰Ω¯––µ»º∂ºÏ—È£¨«Û¡Ωœ‰≤˙µÿ≤ªÕ¨µƒ∏≈¬ £ª
œ‰∆ªπ˚÷–Àʪ˙≥È»°¡Ωœ‰Ω¯––µ»º∂ºÏ—È£¨«Û¡Ωœ‰≤˙µÿ≤ªÕ¨µƒ∏≈¬ £ª
£®3£©”…”⁄ Ð÷÷÷≤πʃ£∫Õ∆ªπ˚∆∑÷ µƒ”∞œÏ£¨‘§º∆√˜ƒÍ≤˙µÿ![]() µƒ –≥°∑ð∂ÓΩ´‘ˆº”
µƒ –≥°∑ð∂ÓΩ´‘ˆº”![]() £¨≤˙µÿ
£¨≤˙µÿ![]() µƒ –≥°∑ð∂ÓΩ´ºı…Ÿ
µƒ –≥°∑ð∂ÓΩ´ºı…Ÿ![]() £¨∆‰À¸≤˙µÿµƒ –≥°∑ð∂Ó≤ª±‰£¨∆ªπ˚œ˙ €º€∏Ò“≤≤ª±‰£®≤ªøº¬«∆‰À¸“ÚÀÿ£©.…ËΩÒƒÍ∆ªπ˚µƒ∆Ωæ˘≈˙∑¢º€Œ™√øœ‰
£¨∆‰À¸≤˙µÿµƒ –≥°∑ð∂Ó≤ª±‰£¨∆ªπ˚œ˙ €º€∏Ò“≤≤ª±‰£®≤ªøº¬«∆‰À¸“ÚÀÿ£©.…ËΩÒƒÍ∆ªπ˚µƒ∆Ωæ˘≈˙∑¢º€Œ™√øœ‰![]() ‘™£¨√˜ƒÍ∆ªπ˚µƒ∆Ωæ˘≈˙∑¢º€Œ™√øœ‰
‘™£¨√˜ƒÍ∆ªπ˚µƒ∆Ωæ˘≈˙∑¢º€Œ™√øœ‰![]() ‘™£¨±»Ωœ
‘™£¨±»Ωœ![]() µƒ¥Û–°.£®÷ª–Ë–¥≥ˆΩ·¬€£©
µƒ¥Û–°.£®÷ª–Ë–¥≥ˆΩ·¬€£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com