
分析 本题是几何概型问题,欲求点M在球O外的概率,先由正方体ABCD-A1B1C1D1内的内切球O,求出其体积,再根据几何概型概率公式结合正方体的体积的方法易求解.
解答 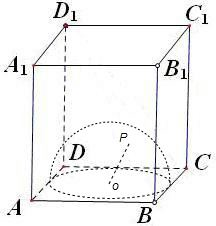 解:本题是几何概型问题,设正方体的棱长为:2.
解:本题是几何概型问题,设正方体的棱长为:2.
正方体ABCD-A1B1C1D1内的内切球O的半径是其棱长的一半,
其体积为:V1=$\frac{4}{3}π×{1}^{3}$=$\frac{4π}{3}$
则点M在球O外的概率是1-$\frac{\frac{4π}{3}}{{2}^{3}}$=1-$\frac{π}{6}$.
故答案为:1-$\frac{π}{6}$.
点评 本小题主要考查几何概型、几何概型的应用、几何体和体积等基础知识,考查空间想象能力、化归与转化思想.属于基础题.


科目:高中数学 来源: 题型:解答题
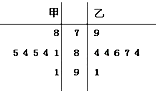 甲、乙两名运动员为了争取得到2016年巴西奥运会的最后一个参赛名额,共进行了7轮比赛,得分情况如茎叶图所示.
甲、乙两名运动员为了争取得到2016年巴西奥运会的最后一个参赛名额,共进行了7轮比赛,得分情况如茎叶图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com