

 +
+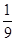 +
+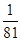 =
=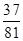 .
. 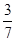 +3×
+3×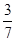 +4×
+4×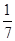 =
=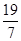 .
. 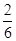 =
= .再分析质点P恰好返回到A点共有三种情况,投掷两次质点P返回到A点,有(1,3)、(3,1)、(2,2)三种结果;投掷三次质点P返回到A点,有 (1,1,2)、(1,2,1)、(2,1,1)三种结果;投掷四次质点P返回到A点,只有 (1,1,1,1).根据相互独立事件和互斥事件的概率公式求解;
.再分析质点P恰好返回到A点共有三种情况,投掷两次质点P返回到A点,有(1,3)、(3,1)、(2,2)三种结果;投掷三次质点P返回到A点,有 (1,1,2)、(1,2,1)、(2,1,1)三种结果;投掷四次质点P返回到A点,只有 (1,1,1,1).根据相互独立事件和互斥事件的概率公式求解;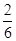 =
= .
. )2×3=
)2×3= ;
; )3×3=
)3×3=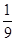 ;
; )4=
)4=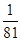 .
. +
+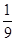 +
+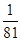 =
=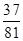 . 6分
. 6分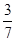 ,P(ξ=3)=
,P(ξ=3)=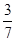 ,P(ξ=4)=
,P(ξ=4)=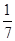 ,
,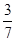 +3×
+3×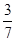 +4×
+4×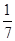 =
=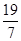 .
.

科目:高中数学 来源:不详 题型:解答题
| 组别 | 理科 | 文科 | ||
| 性别 | 男生 | 女生 | 男生 | 女生 |
| 人数 | 4 | 4 | 3 | 1 |
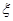 ,求随机变量
,求随机变量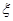 的分布列和数学期望
的分布列和数学期望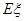 .(8分)
.(8分)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
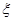 .
.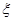 的分布列;
的分布列;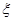 的数学期望);
的数学期望); ,一等品率提高为
,一等品率提高为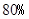 .如果此时要求1件产品的平均利润不小于5.13万元,则三等品率最多是多少?
.如果此时要求1件产品的平均利润不小于5.13万元,则三等品率最多是多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 动作 | K | D | ||
| 得分 | 100 | 80 | 40 | 10 |
| 概率 |  |  |  |  |
| 动作 | K | D | ||
| 得分 | 90 | 50 | 20 | 0 |
| 概率 |  |  |  |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com