
| X | 0 | 1 | x |
| P | 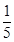 | p | 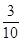 |
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源:不详 题型:解答题
 ,假设每次射击是否命中相互之间没有影响.
,假设每次射击是否命中相互之间没有影响.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,乙队中三人答对的概率分别为
,乙队中三人答对的概率分别为 ,且各人回答得正确与否相互之间没有影响.
,且各人回答得正确与否相互之间没有影响. 表示甲队的总得分,求随机变量
表示甲队的总得分,求随机变量 分布列和数学期望;
分布列和数学期望; 表示事件“甲、乙两队总得分之和为
表示事件“甲、乙两队总得分之和为 ”,用
”,用 表示事件“甲队总得分大于乙队总得分”,求
表示事件“甲队总得分大于乙队总得分”,求 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,求
,求 的分布列及数学期望;
的分布列及数学期望;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 为获得k(k=1,2,3)等奖的折扣率,求随机变量
为获得k(k=1,2,3)等奖的折扣率,求随机变量 的分布列及期望
的分布列及期望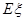 ;(II)若有3人次(投入l球为l人次)参加促销活动,记随机变量
;(II)若有3人次(投入l球为l人次)参加促销活动,记随机变量 为获得1等奖或2等奖的人次,求
为获得1等奖或2等奖的人次,求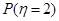 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为 ,
, .
. 的数学期望;
的数学期望;
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,共投篮7次。
,共投篮7次。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com