Question

19．在空间四边形ABCD中，AB=AD，CB=CD．E，F，G，H分别是AB，BC，CD，DA的中点，则下列命题中正确的是（　　）

• A． E，F，G，H四点不共面
• B． EFGH是梯形
• C． EG⊥FH
• D． EFGH是矩形

Answer 1

分析 根据中位线的性质判断EFGH是平行四边形，根据等腰三角形的性质判断垂直关系即可得到结论．

解答 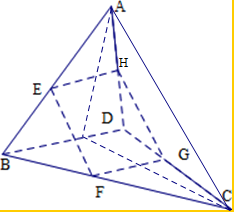解：∵E，F，G，H分别是AB，BC，CD，DA的中点，
∴FG∥BD，EH∥BD，
且FG=$\frac{1}{2}$BD，EH=$\frac{1}{2}$/BD，
即EH∥FG，EH=FG，
即EFGH是平行四边形．
取BD的中点P，则AP⊥BD，CP⊥BD，
∴BD⊥面APC，BD⊥AC．
即EFGH是矩形．
故选：D．

点评 本题考查空间中直线与干线之间的位置关系，解题的关键是掌握空间中直线与直线之间位置关系的判断方法，本题涉及到线线平行的证明，中位线的性质等要注意这些知识在应用时的转化方式．