Question

14．PM2.5是悬浮在空气中的直径小于或等于2.5微米的颗粒物，也成为入肺颗粒物，根据现行国家标准GB3095-2012，PM2.5日均值在35微克/立方米以下空气质量为一级；在35微克/立方米～75微克/立方米之间空气质量为二级；在75微克/立方米以上的空气质量为超标．甲、乙两景区3月2日～3月21日20天内的PM2.5日均值如茎叶图所示：
（Ⅰ）将20天的PM2.5日均值分为五组[0，10），[10，20），[20，30），[30，40），[40，50]试作甲的频率分布直方图，并计算乙景区20天日均值的平均值；
（Ⅱ）已知甲、乙两景区3月6日～9日的PM2.5日均值依次为8、10、15、27；10、13、8、14，某游客欲在相邻的两天分游览甲、乙景区各一天，试求这两天的日均值的差小于5的概率．

Answer 1

分析 （Ⅰ）根据频率分布直方图的画法绘制即可，并根据平均数的定义计算出乙景区20天日均值的平均值；
（Ⅱ）将甲乙两景区的这四天的PM2.5分别即为A₁，A₂，A₃，A₄，B₁，B₂，B₃，B₄，相邻两天游玩两景区的基本事件有6种，其中前两天的PM2.5日均值小于5的事件有4个，
根据概率公式计算即可．

解答 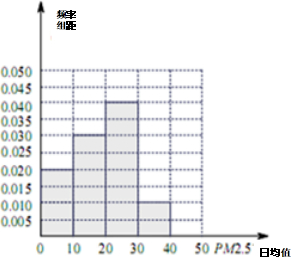解：（Ⅰ）甲的频率分布直方图，
$\overline{x乙}$=25+$\frac{1}{20}$（-16-17-15-12-10-11-2-5+0-3+1+3-1+4+7+11+8+13+15+16）=24.3
（Ⅱ）将甲乙两景区的这四天的PM2.5分别即为A₁，A₂，A₃，A₄，B₁，B₂，B₃，B₄，相邻两天游玩两景区的基本事件有：（A₁B₂），（A₂B₃），（A₃B₄），（B₁A₂），（B₂A₃），（B₃A₄）共6个等可能基本事件，
前两天的PM2.5日均值小于5的事件有（A₂B₃），（A₃B₄），（B₁A₂），（B₂A₃），共4个，
根据古典概型知，其概率为p=$\frac{4}{6}$=$\frac{2}{3}$．

点评 本题考查了频率分布直方图和茎叶图，以及古典概型的概率问题，属于基础题．