
分析 (1)数列1,2,3中保持其中1个元素位置不动的排列只有1,3,2或3,2,1或2,1,3,即可得出;
(2)类比(1)即可得出;
(3):把数列1,2,…,n中任取其中k个元素位置不动,则有$C_n^k$种;其余n-k个元素重新排列,并且使其余n-k个元素都要改变位置,则${P_n}(k)=C_n^k{P_{n-k}}(0)$,可得$\sum_{k=0}^n{k{P_n}(k)}=\sum_{k=0}^nkC_n^k{P_{n-k}}(0)$,利用$kC_n^k=nC_{n-1}^{k-1}$,即可得出.
解答 (1)解:∵数列1,2,3中保持其中1个元素位置不动的排列只有1,3,2或3,2,1或2,1,3,
∴P3(1)=3;
(2)解:$\sum_{k=0}^4{{P_4}(k)}={P_4}(0)+{P_4}(1)+{P_4}(2)+{P_4}(3)+{P_4}(4)$=$C_4^0C_3^1C_3^1+C_4^1C_2^1+C_4^2+0+1=9+8+6+0+1=24$;
(3)证明:把数列1,2,…,n中任取其中k个元素位置不动,则有$C_n^k$种;其余n-k个元素重新排列,并且使其余n-k个元素都要改变位置,则有${P_n}(k)=C_n^k{P_{n-k}}(0)$,
故$\sum_{k=0}^n{k{P_n}(k)}=\sum_{k=0}^nkC_n^k{P_{n-k}}(0)$,
又∵$kC_n^k=nC_{n-1}^{k-1}$,
∴$\sum_{k=0}^n{k{P_n}(k)}=\sum_{k=0}^nkC_n^k{P_{n-k}}(0)=n\sum_{k=0}^{n-1}{C_{n-1}^k{P_{n-k-1}}(0)}=n\sum_{k=0}^{n-1}{{P_{n-1}}(k)}$.
令${a_n}=\sum_{k=0}^n{k{P_n}(k)}$,则an=nan-1,且a1=1.
于是a2a3a4…an-1an=2a1×3a2×4a3×…×nan-1,
左右同除以a2a3a4…an-1,得an=2×3×4×…×n=n!
∴$\sum_{k=0}^n{k{P_n}(k)}=n!$.
点评 本题考查了排列与组合的计算公式及其性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
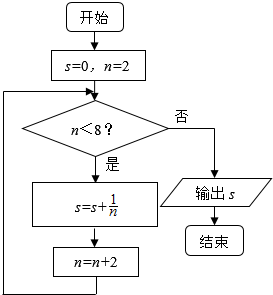 如图所示,程序框图的输出结果是( )
如图所示,程序框图的输出结果是( )| A. | $\frac{1}{16}$ | B. | $\frac{25}{24}$ | C. | $\frac{11}{12}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
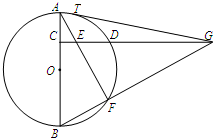 如图,C是⊙O的直径AB上一点,CD⊥AB,与⊙O相交于点D,与弦AF交于点E,与BF的延长线交于点G,GT与⊙O相切于点T.
如图,C是⊙O的直径AB上一点,CD⊥AB,与⊙O相交于点D,与弦AF交于点E,与BF的延长线交于点G,GT与⊙O相切于点T.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 将5个全等的正方形按如图所示方式放置在一个的矩形OEFG内,其中顶点P、C、Q、D分别在矩形的四条边上.
将5个全等的正方形按如图所示方式放置在一个的矩形OEFG内,其中顶点P、C、Q、D分别在矩形的四条边上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
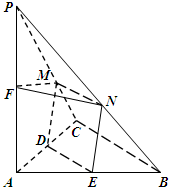 如图,在三棱锥P-ABC中,PA⊥平面ABC,2AC=2BC=PC=2,AC⊥BC,D、E、F分别为AC、AB、AP的中点,M、N分别为线段PC、PB上的动点,且有MN∥BC.
如图,在三棱锥P-ABC中,PA⊥平面ABC,2AC=2BC=PC=2,AC⊥BC,D、E、F分别为AC、AB、AP的中点,M、N分别为线段PC、PB上的动点,且有MN∥BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥α,m⊥β,则α∥β | B. | 若m⊥α,n⊥α,则m∥n | C. | 若α∥γ,β∥γ,则α∥β | D. | 若α⊥γ,β⊥γ,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知AB为半圆O的直径,C为圆弧上一点,过点C作半圆的切线CF,过点A作CF的垂线,垂足为D,AD交半圆于点E,连结EC,BC,AC.
如图,已知AB为半圆O的直径,C为圆弧上一点,过点C作半圆的切线CF,过点A作CF的垂线,垂足为D,AD交半圆于点E,连结EC,BC,AC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | E,F,G,H四点不共面 | B. | EFGH是梯形 | ||
| C. | EG⊥FH | D. | EFGH是矩形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com