
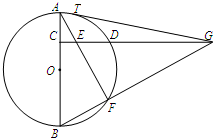
 如图,C是⊙O的直径AB上一点,CD⊥AB,与⊙O相交于点D,与弦AF交于点E,与BF的延长线交于点G,GT与⊙O相切于点T.
如图,C是⊙O的直径AB上一点,CD⊥AB,与⊙O相交于点D,与弦AF交于点E,与BF的延长线交于点G,GT与⊙O相切于点T.分析 (Ⅰ)延长DC与圆O交于点M,利用相交弦定理,结合Rt△ACE∽Rt△GBC,证明:CE•CG=CD2;
(Ⅱ)若AC=CO=1,CD=3CE,求得CG=3CD,利用切割线定理求GT.
解答  (Ⅰ)证明:延长DC与圆O交于点M,
(Ⅰ)证明:延长DC与圆O交于点M,
因为CD⊥AB,
所以CD2=CD•CM=AC•BC,
因为Rt△ACE∽Rt△GBC,所以$\frac{AC}{CE}$=$\frac{CG}{BC}$,
即AC•BC=CE•CG,故CD2=CE•CG.…(5分)
(Ⅱ)解:因为AC=CO=1,所以CD2=AC•BC=3,
又CD=3CE,由(Ⅰ)得CG=3CD,
GT2=GM•GD=(CG+CM)•(CG-CD)=(CG+CD)•(CG-CD)
=CG2-CD2=8CD2=24,故GT=2$\sqrt{6}$.…(10分)
点评 本题考查相交弦定理、切割线定理,考查三角形相似的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
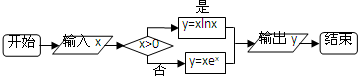
| A. | [-$\frac{1}{e}$,0] | B. | [-$\frac{1}{e}$,0) | C. | [-$\frac{1}{e}$,+∞) | D. | [-$\frac{1}{e}$,e) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com