
| A. | [-$\frac{1}{e}$,0] | B. | [-$\frac{1}{e}$,0) | C. | [-$\frac{1}{e}$,+∞) | D. | [-$\frac{1}{e}$,e) |
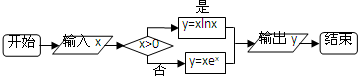
分析 根据题意,模拟程序框图的运行过程,即可得出正确的答案.
解答  解:模拟程序框图的运行过程,知该程序运行的结果是输出函数y=$\left\{\begin{array}{l}{xlnx}&{x>0}\\{x{e}^{x}}&{x≤0}\end{array}\right.$;
解:模拟程序框图的运行过程,知该程序运行的结果是输出函数y=$\left\{\begin{array}{l}{xlnx}&{x>0}\\{x{e}^{x}}&{x≤0}\end{array}\right.$;
当x∈(-∞,0]时,y=xex∈[-$\frac{1}{e}$,0];
当x∈(0,1]时,y=xlnx∈[-$\frac{1}{e}$,0];
∴输出的y∈[-$\frac{1}{e}$,0].
故选:A.
点评 本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的答案,属于基本知识的考查.


科目:高中数学 来源: 题型:解答题
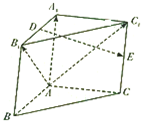 如图,在三棱柱ABC-A1B1C1中,A1A⊥底面ABC,AB⊥AC,E分别是A1B1,CC1的中点.
如图,在三棱柱ABC-A1B1C1中,A1A⊥底面ABC,AB⊥AC,E分别是A1B1,CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π-4}{4}$ | B. | $\frac{π-2}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{4-π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
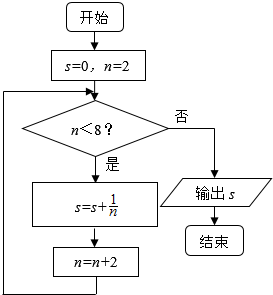 如图所示,程序框图的输出结果是( )
如图所示,程序框图的输出结果是( )| A. | $\frac{1}{16}$ | B. | $\frac{25}{24}$ | C. | $\frac{11}{12}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
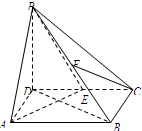 如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2,AD=$\sqrt{2}$,PD⊥平面ABCD,E,F分别为CD,PB的中点.求证:
如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2,AD=$\sqrt{2}$,PD⊥平面ABCD,E,F分别为CD,PB的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
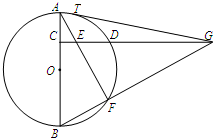 如图,C是⊙O的直径AB上一点,CD⊥AB,与⊙O相交于点D,与弦AF交于点E,与BF的延长线交于点G,GT与⊙O相切于点T.
如图,C是⊙O的直径AB上一点,CD⊥AB,与⊙O相交于点D,与弦AF交于点E,与BF的延长线交于点G,GT与⊙O相切于点T.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥α,m⊥β,则α∥β | B. | 若m⊥α,n⊥α,则m∥n | C. | 若α∥γ,β∥γ,则α∥β | D. | 若α⊥γ,β⊥γ,则α∥β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com