
���� ��I����ƽ�����������������㼰���Ǻ����еĺ�ȱ任Ӧ�ÿɵ�f��x��=2sin��2x-$\frac{��}{6}$�����Ӷ�������f��x������С�����ڣ�
��$x��[{\frac{��}{12}��\frac{2��}{3}}]$ʱ������-$\frac{��}{3}��$2x-$\frac{��}{6}$$��\frac{7��}{6}$���Ӷ��ɵ�f��x����ȡֵ��Χ��
���������Ǻ����еĺ�ȱ任Ӧ�ÿ���g��x��=2cos2x����g��$\frac{A}{2}$��=2cosA=1����Ϸ�Χ0�������У�����A��ֵ�������Ҷ�������bc���Ӷ��������������ʽ���ɵý⣮
��� �⣺��I����f��x��=$\overrightarrow{a}$•$\overrightarrow{b}$+1=2$\sqrt{3}$sinxcosx-2cos2x+1=$\sqrt{3}$sin2x-cos2x=2sin��2x-$\frac{��}{6}$����
�ຯ��f��x������С������T=$\frac{2��}{2}=��$��
��$x��[{\frac{��}{12}��\frac{2��}{3}}]$ʱ��-$\frac{��}{3}��$2x-$\frac{��}{6}$$��\frac{7��}{6}$������-$\frac{1}{2}$��sin��2x-$\frac{��}{6}$����1��
��f��x����ȡֵ��ΧΪ��[-1��2]��6��
����g��x��=f��x+$\frac{��}{3}$��=2sin[2��x+$\frac{��}{3}$��-$\frac{��}{6}$]=2sin��2x+$\frac{��}{2}$��=2cos2x��
��g��$\frac{A}{2}$��=2cosA=1��cosA=$\frac{1}{2}$��
��0����������A=$\frac{��}{3}$��
�ڡ�ABC�У�a2=b2+c2-2bccosA��
��4=b2+c2-2bc$•\frac{1}{2}$��
��4=��b+c��2-2bc-bc��4=16-3bc��
��bc=4
��S��ABC=$\frac{1}{2}$bcsinA=$\sqrt{3}$��12��
���� ������Ҫ�����˺���y=Asin����x+�գ���ͼ��任��ƽ�����������������㣬���Ǻ����еĺ�ȱ任Ӧ�ã��ۺ��Խ�ǿ�����ڻ���֪ʶ�Ŀ��飮


 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
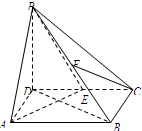 ��ͼ��������P-ABCD�У�����ABCD�Ǿ��Σ�AB=2��AD=$\sqrt{2}$��PD��ƽ��ABCD��E��F�ֱ�ΪCD��PB���е㣮��֤��
��ͼ��������P-ABCD�У�����ABCD�Ǿ��Σ�AB=2��AD=$\sqrt{2}$��PD��ƽ��ABCD��E��F�ֱ�ΪCD��PB���е㣮��֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
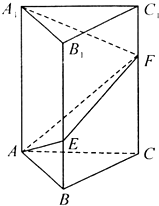 ��ͼ����ֱ������ABC-A1B1C1�У���֪��BAC=90�㣬AB=AC=1��AA1=3����E��F�ֱ�����BB1��CC1�ϣ���C1F=$\frac{1}{3}$C1C��BE=$\frac{1}{3}$BB1��
��ͼ����ֱ������ABC-A1B1C1�У���֪��BAC=90�㣬AB=AC=1��AA1=3����E��F�ֱ�����BB1��CC1�ϣ���C1F=$\frac{1}{3}$C1C��BE=$\frac{1}{3}$BB1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
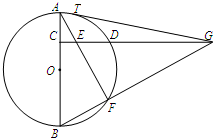 ��ͼ��C�ǡ�O��ֱ��AB��һ�㣬CD��AB�����O�ཻ�ڵ�D������AF���ڵ�E����BF���ӳ��߽��ڵ�G��GT���O�����ڵ�T��
��ͼ��C�ǡ�O��ֱ��AB��һ�㣬CD��AB�����O�ཻ�ڵ�D������AF���ڵ�E����BF���ӳ��߽��ڵ�G��GT���O�����ڵ�T���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | $\sqrt{2}$��$-\sqrt{2}$ | C�� | $-\sqrt{2}$ | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $f��{-\frac{1}{2}}����f��{\frac{3}{4}}����f��{\frac{2}{3}}��$ | B�� | $f��{-\frac{1}{2}}����f��{\frac{2}{3}}����f��{\frac{3}{4}}��$ | C�� | $f��{\frac{3}{4}}����f��{\frac{2}{3}}����f��{-\frac{1}{2}}��$ | D�� | $f��{\frac{2}{3}}����f��{-\frac{1}{2}}����f��{\frac{3}{4}}��$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com