已知函数f(x)=aln(1+ex)-(a+1)x,(其中a>0),点A(x1,f(x1),,B)C(x3,f(x3))从左到右依次是函数y=f(x)图象上的不同点,且x1,x2,x3成等差数列.
(1)证明:函数f(x)在R上是单调递减函数;
(2)证明:△ABC为钝角三角形;
(3)请问△ABC能否成为等腰三角形?若能,求△ABC面积的最大值;若不能,说明理由.
【答案】
分析:(1)∵f(x)=aln(1+e
x)-(a+1)x,欲证函数f(x)在(-∞,+∞)上是单调减函数,只须证明其导数f′(x)<0即可;
(2)先设A(x
1,f(x
1)),B(x
2,f(x
2)),C(x
3,f(x
3))且x
1<x
2<x
3,欲证:△ABC是钝角三角形,只须证明其中一个内角为钝角即可,结合向量的坐标运算,只须证明:
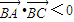
即得;
(3)假设△ABC为等腰三角形,则只能是
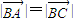
,再利用平面内两点的距离公式将点的坐标代入计算,如出现矛盾,则△ABC不可能为等腰三角形,如不矛盾,则△ABC能是等腰三角形.
解答:解:(1)∵f(x)=aln(1+e
x)-(a+1)x,∴
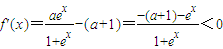
恒成立,
所以函数f(x)在(-∞,+∞)上是单调减函数.(3分)
(2)证明:据题意A(x
1,f(x
1)),B(x
2,f(x
2)),C(x
3,f(x
3))且x
1<x
2<x
3,
由(Ⅰ)知f(x
1)>f(x
2)>f(x
3),x
2=
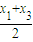
(4分)
可得A(x
1,f(x
1)),B(x
2,f(x
2)),C(x
3,f(x
3))三点不共线
(反证法:否则
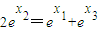

,得x
1=x
3)
∴
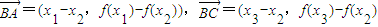
∴
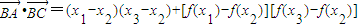
(6分)
∵x
1-x
2<0,x
3-x
2>0,f(x
1)-f(x
2)>0,f(x
3)-f(x
2)<0,∴
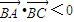
,∴
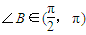
即△ABC是钝角三角形(8分)
(3)假设△ABC为等腰三角形,则只能是
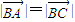
即:(x
1-x
2)
2+[f(x
1)-f(x
2)]
2=(x
3-x
2)
2+[f(x
3)-f(x
2)]
2∵x
2-x
1=x
3-x
2∴[f(x
1)-f(x
2)]
2=[f(x
3)-f(x
2)]
2即2f(x
2)=f(x
1)+f(x
3)
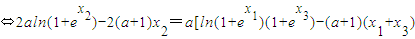
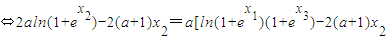
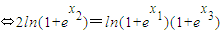


①(11分)
而事实上,
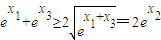
②
由于

,故(2)式等号不成立.这与(1)式矛盾.
所以△ABC不可能为等腰三角形.(13分)
点评:此题是个难题.本小题主要考查利用导数研究函数的单调性、数量积表示两个向量的夹角、两点间距离公式的应用等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想,同时考查学生灵活应用知识分析解决问题的能力和计算能力.

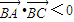 即得;
即得;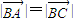 ,再利用平面内两点的距离公式将点的坐标代入计算,如出现矛盾,则△ABC不可能为等腰三角形,如不矛盾,则△ABC能是等腰三角形.
,再利用平面内两点的距离公式将点的坐标代入计算,如出现矛盾,则△ABC不可能为等腰三角形,如不矛盾,则△ABC能是等腰三角形.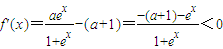 恒成立,
恒成立,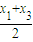 (4分)
(4分)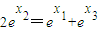
 ,得x1=x3)
,得x1=x3)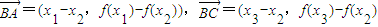
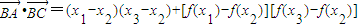 (6分)
(6分)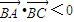 ,∴
,∴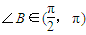
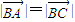
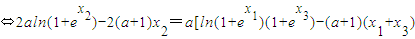
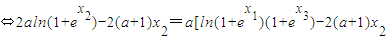
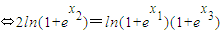

 ①(11分)
①(11分)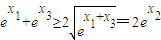 ②
② ,故(2)式等号不成立.这与(1)式矛盾.
,故(2)式等号不成立.这与(1)式矛盾.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案