
分析 (Ⅰ)每个同学被抽到的概率为$\frac{1}{15}$,由此利用分层抽样方法能求出课外兴趣小组中男、女同学人数.
(Ⅱ)这个兴趣小组决定随机选出两名同学分别去做某项试验,先求出基本事件总数,再求出选出的两名同学中恰有一名女同学包含的基本事件个数,由此能求出选出的两名同学中恰有一名女同学的概率.
解答 解:(Ⅰ)∵p=$\frac{5}{75}$=$\frac{1}{15}$,∴每个同学被抽到的概率为$\frac{1}{15}$,
∴课外兴趣小组中男同学人数为:45×$\frac{1}{15}$=3人,
女同学的人数为:30×$\frac{1}{15}$=2人.
(Ⅱ)这个兴趣小组决定随机选出两名同学分别去做某项试验,
基本事件总数n=${C}_{5}^{2}$=10,
选出的两名同学中恰有一名女同学包含的基本事件个数m=${C}_{2}^{1}{C}_{3}^{1}$=6,
∴选出的两名同学中恰有一名女同学的概率为p=$\frac{6}{10}=\frac{3}{5}$.
点评 本题考查分层抽样方法的应用,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
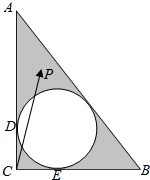 在Rt△ABC中,∠C是直角,CA=4,CB=3,△ABC的内切圆交CA,CB于点D,E,点P是图中阴影区域内的一点(不包含边界).若$\overrightarrow{CP}$=x$\overrightarrow{CD}$+y$\overrightarrow{CE}$,则x+y的值可以是( )
在Rt△ABC中,∠C是直角,CA=4,CB=3,△ABC的内切圆交CA,CB于点D,E,点P是图中阴影区域内的一点(不包含边界).若$\overrightarrow{CP}$=x$\overrightarrow{CD}$+y$\overrightarrow{CE}$,则x+y的值可以是( )| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示的三角形数阵叫“牛顿调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,=$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,…,
如图所示的三角形数阵叫“牛顿调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,=$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,…,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解我市高二年级进行的一次考试中数学成绩的分布状况,有关部门随机抽取了一个样本,对数学成绩进行分组统计分析如下表:
为了解我市高二年级进行的一次考试中数学成绩的分布状况,有关部门随机抽取了一个样本,对数学成绩进行分组统计分析如下表:| 分组 | 频数 | 频率 |
| [0,30) | 3 | 0.03 |
| [30,60) | 3 | 0.03 |
| [60,90) | 37 | 0.37 |
| [90,120) | m | n |
| [120,150) | 15 | 0.15 |
| 合计 | M | N |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com