Question

14．为了解我市高二年级进行的一次考试中数学成绩的分布状况，有关部门随机抽取了一个样本，对数学成绩进行分组统计分析如下表：
（1）求出表中m、n、M、N的值，并根据表中所给数据在下面给出的坐标系中画出频率分布直方图：

分组	频数	频率
[0，30）	3	0.03
[30，60）	3	0.03
[60，90）	37	0.37
[90，120）	m	n
[120，150）	15	0.15
合计	M	N

（2）若我市参加本次考试的学生有18000人，试估计这次测试中我市学生成绩在90分以上的人数；
（3）为了深入分析学生的成绩，有关部门拟从分数不超过60的学生中选取2人进行进一步分析，求被选中2人分数均不超过30分的概率．

Answer 1

分析 （I）由频率分布表利用频率=$\frac{频数}{总数}$，能求出M，m，n，前能出频率分布直方图示．
（Ⅱ）先求出全区90分以上学生的频率，由此能估计这次测试中我市学生成绩在90分以上的人数．
（Ⅲ）利用列举法能求出被选中2人分数均不超过30分的概率．

解答 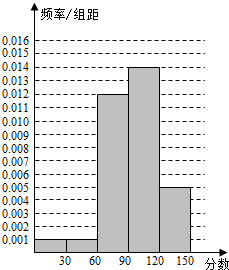解：（I）由频率分布表得M=$\frac{3}{0.03}$=100，
∴m=100-（3+3+37+15）=42，
n=$\frac{42}{100}$=0.42，N=0.03+0.03+0.37+0.42+0.15=1，
频率分布表如右图所示．
（Ⅱ）由题意知，全区90分以上学生估计为$\frac{42+15}{100}×18000=10260$（人）．
（Ⅲ）设考试成绩在（0，30]内的3 人分别为A、B、C，考试成绩在（30，60]内的3人分别为a，b，c，
从不超过60分的6人中，任意取2人的结果有15个：
（A，B），（A，C），（A，a），（A，b），（A，c），（B，C），（B，a），（B，b），（B，c），（C，a），（C，b），（C，c），（a，b），（a，c），（b，c），
被选中2人分数均不超过30分的情况有：（A，B），（A，C），（B，C），共3个，
∴被选中2人分数均不超过30分的概率p=$\frac{3}{15}=\frac{1}{5}$．

点评 本题考查概率的求法，是基础题，解题时要认真审题，注意频率分布直方图和列举法的合理运用．