
分析 (1)S10=a1+a2+…+a10=55,求得55d=55,可解得a1=d=1,写出通项公式和前n项和公式;
(2)由(1)写出数列{bn}的通项公式,采用裂项法求出Tn的值,可判断Tn的取值范围.
解答 解:(Ⅰ)设数列{an}的公差为d,则a1=d,an=a1+(n-1)d=nd,
由S10=a1+a2+…+a10=55d=55,解得d=1,
所以an=n,则${S_n}=\frac{1+n}{2}×n=\frac{1}{2}n(n+1)$.(4分)
(Ⅱ)可得${b_n}=\frac{2}{n(n+1)}=2(\frac{1}{n}-\frac{1}{n+1})$,(6分)
所以${T_n}=2(\frac{1}{1}-\frac{1}{2})+2(\frac{1}{2}-\frac{1}{3})+2(\frac{1}{3}-\frac{1}{4})+…+2({\frac{1}{n}-\frac{1}{n+1}})=2(1-\frac{1}{n+1})=\frac{2n}{n+1}$,(8分)
由于$2(1-\frac{1}{n+1})$为随n的增大而增大,可得1≤Tn<2.
即Tn的取值范围是[1,2).(12分)
点评 本题考查等差数列的通项公式和前n项和公式及采用裂项法求数列的前n项和,过程简单,属于中档题.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{2}$,+∞) | B. | (1,$\frac{1}{e}$) | C. | [e,+∞) | D. | (e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
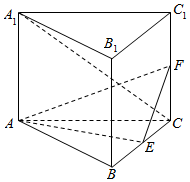 如图所示,正三棱柱ABC-A1B1C1中,E,F分别是BC,CC1的中点.
如图所示,正三棱柱ABC-A1B1C1中,E,F分别是BC,CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(5)-f(3)>0 | B. | f(6)-f(2)<0 | C. | 4f(2)-f(3)<0 | D. | 4f(6)-f(5)>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,0) | B. | (-∞,-2) | C. | (-8,0) | D. | (0,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com