
| A. | f(5)-f(3)>0 | B. | f(6)-f(2)<0 | C. | 4f(2)-f(3)<0 | D. | 4f(6)-f(5)>0 |
分析 由所给不等式2f(x)-(4-x)f′(x)>0恒成立,构造辅助函数g(x)=(x-4)2f(x),由辅助函数求导,知g′(x)=(x-4)[2f(x)-(4-x)f′(x)],与所给不等式有关,所以由辅助函数的单调性可知对应的f(x)的值的大小.
解答 解:∵2f(x)-(4-x)f′(x)>0,
∴作辅助函数g(x)=(x-4)2f(x),
则g′(x)=(x-4)[2f(x)-(4-x)f′(x)],
当x>4时,有x-4>0,2f(x)-(4-x)f′(x)>0,
∴g(x)在[4,+∞)上是增函数.
∴当5<6时,有g(5)<g(6),即f(5)<4f(6),
∴4f(6)-f(5)>0.
故选:D.
点评 本题考查由所给不等式,构造辅助函数,对辅助函数求导,知与所给不等式有关,所以由辅助函数的单调性可知对应的f(x)的值的大小.属于好题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| i | 1 | 2 | 3 |
| F(i) | 2 | 3 | 1 |
| i | 1 | 2 | 3 | 4 |
| F(i) | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
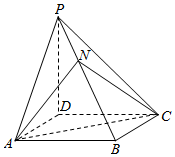 如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与三棱锥D-PAC的体积比为( )
如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与三棱锥D-PAC的体积比为( )| A. | 1:2 | B. | 1:8 | C. | 1:6 | D. | 1:3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{4}$,+∞) | B. | (-∞,-$\frac{1}{4}$) | C. | (0,+∞) | D. | (-∞,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,是某铁路客运部门设计的甲、乙两地之间旅客托运行李的费用c(单位:元)与行李重量w(单位:千克)之间的流程图.假定某旅客的托运费为10元,则该旅客托运的行李重量为20千克.
如图,是某铁路客运部门设计的甲、乙两地之间旅客托运行李的费用c(单位:元)与行李重量w(单位:千克)之间的流程图.假定某旅客的托运费为10元,则该旅客托运的行李重量为20千克.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com