
分析 对|k$\overrightarrow{a}$$+\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$-k$\overrightarrow{b}$|两边平方,得出$\overrightarrow{a}•\overrightarrow{b}$关于k的函数,利用基本不等式即可求出最小值.
解答 解:|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,
∵|k$\overrightarrow{a}$$+\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$-k$\overrightarrow{b}$|,∴k2+2k$\overrightarrow{a}•\overrightarrow{b}$+1=3(1-2k$\overrightarrow{a}•\overrightarrow{b}$+k2).
即k2-4$\overrightarrow{a}•\overrightarrow{b}$+1=0.
∴$\overrightarrow{a}•\overrightarrow{b}$=$\frac{{k}^{2}+1}{4k}$=$\frac{k}{4}+\frac{1}{4k}$≥2$\sqrt{\frac{1}{16}}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了平面向量的数量级运算,基本不等式的应用,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,则|$\overrightarrow{a}$|-|$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$| | B. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$| | ||
| C. | 若|$\overrightarrow{a}$|-|$\overrightarrow{b}$|<|$\overrightarrow{a}$+$\overrightarrow{b}$|,则$\overrightarrow{a}$,$\overrightarrow{b}$不共线 | D. | 若$\overrightarrow{a}$,$\overrightarrow{b}$不共线,则|$\overrightarrow{a}$+$\overrightarrow{b}$|<|$\overrightarrow{a}$|+|$\overrightarrow{b}$| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
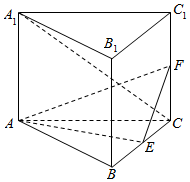 如图所示,正三棱柱ABC-A1B1C1中,E,F分别是BC,CC1的中点.
如图所示,正三棱柱ABC-A1B1C1中,E,F分别是BC,CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(5)-f(3)>0 | B. | f(6)-f(2)<0 | C. | 4f(2)-f(3)<0 | D. | 4f(6)-f(5)>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | 2i | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com