
分析 因为“p且q”为假命题,所以p真q假或p假q真或都为假命题.
解答 解:∵命题p:函数y=ax(a>0,且a≠1)为R上的单调递减函数,
∴0<a<1;
∵命题q:函数y=lg(ax2-x+a)值域为R,
∴△=≥0,
∴-$\frac{1}{2}$<a<$\frac{1}{2}$
若“p且q”为假,
所以:a≥$\frac{1}{2}$
点评 本题考查了“或”命题和“且”命题的真假性,关键是弄清两种命题的构成,及各部分的真假性.所有情况如下:
(1)p∧q为真的情况有:p真,且q真;p∧q为假的情况有:①p真,且q假,②p假,且q真,③p假,且q假,即“两真才真,一假为假”.
(2)p∨q为真的情况有:①p真,且q假,②p假,且q真,③p真,且q真;p∨q为假的情况有:p假,且q假,即“一真为真,两假才假”.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| i | 1 | 2 | 3 |
| F(i) | 2 | 3 | 1 |
| i | 1 | 2 | 3 | 4 |
| F(i) | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
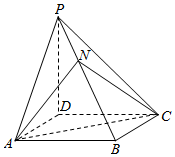 如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与三棱锥D-PAC的体积比为( )
如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与三棱锥D-PAC的体积比为( )| A. | 1:2 | B. | 1:8 | C. | 1:6 | D. | 1:3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{4}$,+∞) | B. | (-∞,-$\frac{1}{4}$) | C. | (0,+∞) | D. | (-∞,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com