
| i | 1 | 2 | 3 |
| F(i) | 2 | 3 | 1 |
| i | 1 | 2 | 3 | 4 |
| F(i) | 3 |
分析 (1)根据“优映射”的定义可得,
| i | 1 | 2 | 3 | 4 |
| f(i) | 2 | 3 | 1 | 4 |
| i | 1 | 2 | 3 | 4 |
| f(i) | 2 | 3 | 4 | 1 |
解答 解:(1)
| i | 1 | 2 | 3 | 4 |
| f(i) | 2 | 3 | 1 | 4 |
| i | 1 | 2 | 3 | 4 |
| f(i) | 2 | 3 | 4 | 1 |
点评 本题考查映射的定义,“优映射”的定义,判断f(1)≠1,是解题的关键,是一道不错的创新题,属中档题.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
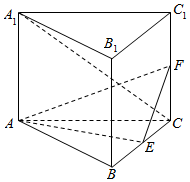 如图所示,正三棱柱ABC-A1B1C1中,E,F分别是BC,CC1的中点.
如图所示,正三棱柱ABC-A1B1C1中,E,F分别是BC,CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(5)-f(3)>0 | B. | f(6)-f(2)<0 | C. | 4f(2)-f(3)<0 | D. | 4f(6)-f(5)>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com