
分析 (1)由题意求出$\overline{x}$,$\overline{y}$,根据$\sum_{i=1}^{5}{x}_{i}^{2}$,$\sum_{i=1}^{5}{x}_{i}{y}_{i}$,代入公式求值$\widehat{b}$,又由$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,得出$\widehat{a}$从而得到回归直线方程;
(2)变量y的值随x的值增加而增加,可知x与y之间是正相关还是负相关.
(3)代入x=7即可预测该家庭的月储蓄.
解答 解:(1)由题意知,n=10,$\sum_{i=1}^{10}$xi=80,$\sum_{i=1}^{10}$yi=20,
∴$\overline{x}$=$\frac{80}{10}=8$,$\overline{y}$=$\frac{20}{10}=2$
那么:n•$\overline{x}$•$\overline{y}$=10×8×2=160,n•$\overline{x}$2=10×64=640.
$\sum_{i=1}^{10}$xiyi=184,$\sum_{i=1}^{10}$x${\;}_{i}^{2}$=720.
由$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n\overline{{x}^{2}}}$=$\frac{184-160}{720-640}=0.3$.
$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=2-0.3×8=-0.4,
故所求回归方程为y=0.3x-0.4.
(2)由于变量y的值随x的值增加而增加,即$\widehat{b}$=0.3>0.
故x与y之间是正相关.
(3)将x=7代入回归方程可以预测该家庭的月储蓄为y=0.3×7-0.4=1.7(千元).
点评 本题考查了线性回归方程的求法及应用,属于基础题.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:选择题
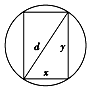 如图,横梁的横断面是一个矩形,而横梁的强度和它的矩形横断面的宽与高的平方的乘积成正比,要将直径为d的圆木锯成强度最大的横梁,则横断面的高和宽分别为( )
如图,横梁的横断面是一个矩形,而横梁的强度和它的矩形横断面的宽与高的平方的乘积成正比,要将直径为d的圆木锯成强度最大的横梁,则横断面的高和宽分别为( )| A. | $\sqrt{3}$d,$\frac{\sqrt{3}}{3}$d | B. | $\frac{\sqrt{3}}{3}$d,$\frac{\sqrt{6}}{3}$d | C. | $\frac{\sqrt{6}}{3}$d,$\frac{\sqrt{3}}{3}$d | D. | $\frac{\sqrt{6}}{3}$d,$\sqrt{3}$d |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知△ABC中,D是BC的中点,$\overrightarrow{AE}=2\overrightarrow{EB}$,AD和CE相交于点P,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$.
已知△ABC中,D是BC的中点,$\overrightarrow{AE}=2\overrightarrow{EB}$,AD和CE相交于点P,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2cos2x | B. | y=2sin2x | C. | y=1+sin(2x+$\frac{π}{4}$) | D. | y=cos2x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{5}{6}$ | C. | -$\frac{3}{4}$ | D. | $\frac{6}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com