
| A. | λ=-1 | B. | λ=$\frac{1}{2}$ | C. | λ=$\frac{5}{8}$ | D. | λ=$\frac{7}{16}$ |
分析 可设t=log2x(0≤t≤1),即有g(t)=2t2-4λt-1在[0,1]上的最小值是-$\frac{3}{2}$,求出对称轴,讨论对称轴和区间[0,1]的关系,运用单调性可得最小值,解方程可得所求值.
解答 解:可设t=log2x(0≤t≤1),
即有g(t)=2t2-4λt-1在[0,1]上的最小值是-$\frac{3}{2}$,
对称轴为t=λ,
①当λ≤0时,[0,1]为增区间,即有g(0)为最小值,且为-1,不成立;
②当λ≥1时,[0,1]为减区间,即有g(1)为最小值,
且为1-4λ=-$\frac{3}{2}$,解得λ=$\frac{5}{8}$,不成立;
③当0<λ<1时,[0,λ)为减区间,(λ,1)为增区间,
即有g(λ)取得最小值,且为2λ2-4λ2-1=-$\frac{3}{2}$,解得λ=$\frac{1}{2}$(负的舍去).
综上可得,$λ=\frac{1}{2}$.
故选B.
点评 本题考查可化为二次函数的最值的求法,注意运用换元法和对数函数的单调性,讨论二次函数的对称轴和区间的关系,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (0,2) | C. | (0,$\frac{2}{3}$) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
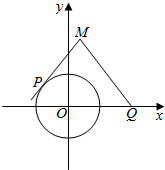 已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1.动点M到圆的切线长等于|MQ|的2倍.
已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1.动点M到圆的切线长等于|MQ|的2倍.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com