
分析 (1)求出P点坐标,设出切点坐标,根据导数的几何意义列出方程求出切点坐标和切线效率,代入点斜式方程;
(2)求出l与C2的交点坐标,使用定积分求出封闭图形的面积.
解答 解:(1)解方程组$\left\{\begin{array}{l}{y={x}^{2}}\\{{y}^{2}=x}\\{x>0}\\{y>0}\end{array}\right.$得x=y=1,∴P(1,1).
设f(x)=x2,则f′(x)=2x,
设l与C1的切点为(x0,x02),则切线斜率为k=f′(x0)=2x0,
∴l的方程为$y-x_0^2=2{x_0}(x-{x_0})$,把P(1,1)代入l方程得,x0=1,
∴切线l方程为2x-y-1=0.
(2)解方程组$\left\{\begin{array}{l}{2x-y-1=0}\\{{y}^{2}=x}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{1}{4}}\\{y=-\frac{1}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
∴S=${∫}_{-\frac{1}{2}}^{1}(\frac{y+1}{2}-{y}^{2})dy$=($\frac{{y}^{2}}{4}$+$\frac{1}{2}y$-$\frac{{y}^{3}}{3}$)${|}_{-\frac{1}{2}}^{1}$=$\frac{9}{16}$.
点评 本题考查了导数的几何意义,定积分在求面积中的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | (1,3) | C. | (1,+∞) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
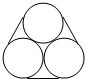 李师傅在建材商店购买了三根外围直径都为10cm的钢管,为了便于携带,他将三根钢管用铁丝紧紧捆住,截面如图所示,则铁丝捆扎一圈的长度为30+10πcm.
李师傅在建材商店购买了三根外围直径都为10cm的钢管,为了便于携带,他将三根钢管用铁丝紧紧捆住,截面如图所示,则铁丝捆扎一圈的长度为30+10πcm.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | λ=-1 | B. | λ=$\frac{1}{2}$ | C. | λ=$\frac{5}{8}$ | D. | λ=$\frac{7}{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com