
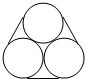
 李师傅在建材商店购买了三根外围直径都为10cm的钢管,为了便于携带,他将三根钢管用铁丝紧紧捆住,截面如图所示,则铁丝捆扎一圈的长度为30+10πcm.
李师傅在建材商店购买了三根外围直径都为10cm的钢管,为了便于携带,他将三根钢管用铁丝紧紧捆住,截面如图所示,则铁丝捆扎一圈的长度为30+10πcm. 科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\frac{5}{3}]$ | B. | (0,1) | C. | (1,+∞) | D. | $[\frac{5}{3},2)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (0,2) | C. | (0,$\frac{2}{3}$) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
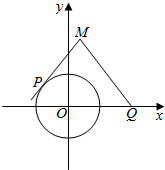 已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1.动点M到圆的切线长等于|MQ|的2倍.
已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1.动点M到圆的切线长等于|MQ|的2倍.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com