
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据最小二乘法原理和回归系数公式进行判断.
解答 解:由回归系数公式$\stackrel{∧}{a}$=$\overline{y}-\stackrel{∧}{b}\overline{x}$可知(1)正确;由回归系数公式$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$可知(3)正确;
由最小二乘法原理可知(4)正确,(2)不正确.
故选:C.
点评 本题考查了最小二乘法求回归方程原理,属于基础题.


科目:高中数学 来源: 题型:填空题
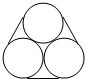 李师傅在建材商店购买了三根外围直径都为10cm的钢管,为了便于携带,他将三根钢管用铁丝紧紧捆住,截面如图所示,则铁丝捆扎一圈的长度为30+10πcm.
李师傅在建材商店购买了三根外围直径都为10cm的钢管,为了便于携带,他将三根钢管用铁丝紧紧捆住,截面如图所示,则铁丝捆扎一圈的长度为30+10πcm.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}<a<2$ | B. | $\frac{5}{4}≤a≤2$ | C. | $2≤a≤\frac{7}{2}$ | D. | $2<a<\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
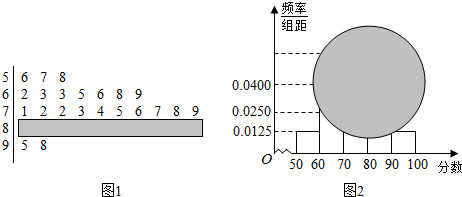
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | λ=-1 | B. | λ=$\frac{1}{2}$ | C. | λ=$\frac{5}{8}$ | D. | λ=$\frac{7}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com