
���� ��1������ֱ��l�IJ������̣����οɵ�ֱ��l����ͨ���̣���������C����ͨ���̣���x=��cos�ȣ�y=��sin�ȣ����뻯�ɵ�����C�ļ����귽�̣�
��2���������l�����ͨ����Ϊy=x�������伫���귽��Ϊ��=$\frac{��}{4}$������C�ļ����귽�̣��ɵ��ҳ���������ľ࣬�ɵ������������
��� �⣺��1����ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=-1+t}\\{y=1+t}\end{array}\right.$��
��t=x+1����y=1+t�ã�
ֱ��l����ͨ����Ϊy=x+2��
������C����ͨ����Ϊ��x-2��2+��y-1��2=5��
������C�ļ����귽��Ϊ����cos��-2��2+����sin��-1��2=5��
����=4cos��+2sin�ȡ���5�֣�
��2����ֱ��l����ƽ��2����λ�õ�ֱ��l�䣬
��l�����ͨ����Ϊy=x��
�����伫���귽��Ϊ��=$\frac{��}{4}$��
�����=4cos��+2sin�ȵã���=3$\sqrt{2}$��
��|AB|=3$\sqrt{2}$��
��ΪOP��l�䣬���Ե�P��ֱ��l��ľ���Ϊ2$\sqrt{2}$��
���ԡ�PAB�����S=$\frac{1}{2}$��3$\sqrt{2}$��2$\sqrt{2}$=6����10�֣�
���� ���⿼���֪ʶ���Ǽ����ߵļ����귽�̣�������������ͨ���̵Ļ����������������ʽ���Ѷ��е���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 20x=M | B�� | 20x=M��1+5%��20 | C�� | 20x��M��1+5%��20 | D�� | 20x��M��1+5%��20 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
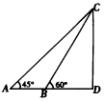 ��ͼ��ʾ��A��B��D�ڵ�ƽ��ͬһֱ���ϣ�AB=20����A��B���ز��C������Ƿֱ�Ϊ45���60�㣬��C�������ĸ�CD���ڣ�������
��ͼ��ʾ��A��B��D�ڵ�ƽ��ͬһֱ���ϣ�AB=20����A��B���ز��C������Ƿֱ�Ϊ45���60�㣬��C�������ĸ�CD���ڣ�������| A�� | $10��\sqrt{3}-1��$ | B�� | $10��\sqrt{3}+1��$ | C�� | $10��3-\sqrt{3}��$ | D�� | $10��3+\sqrt{3}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��sin$\frac{��}{5}$����f��cos$\frac{��}{5}$�� | B�� | f��sin$\frac{��}{5}$����f��cos$\frac{��}{5}$�� | C�� | f��sin$\frac{��}{5}$��=f��cos$\frac{��}{5}$�� | D�� | ��С��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��x��=x-1��g��x��=$\frac{x^2}{x}$-1 | B�� | f��x��=2x-1��g��x��=2x+1 | ||
| C�� | f��x��=x2��g��x��=$\root{3}{{x}^{6}}$ | D�� | f��x��=1��g��x��=x0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
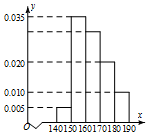 ij�����꼶��500��ͬѧ�������ǵ����ߣ���λ��cm�����ݻ��Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ������������[160��170����[170��180����[180��190]�����ڵ�ѧ���У��÷ֲ�����ķ���ѡȡ30�˲μ�һ�������������[160��170���ڵ�ѧ����ѡȡ������ӦΪ15��
ij�����꼶��500��ͬѧ�������ǵ����ߣ���λ��cm�����ݻ��Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ������������[160��170����[170��180����[180��190]�����ڵ�ѧ���У��÷ֲ�����ķ���ѡȡ30�˲μ�һ�������������[160��170���ڵ�ѧ����ѡȡ������ӦΪ15���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=x2 | B�� | y=ex | C�� | y=log0.5|x| | D�� | y=sinx |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com