
分析 (1)利用两个向量的坐标形式的运算,两个向量的数量积公式,求得($\overrightarrow a+\overrightarrow b$)•($\overrightarrow a-\overrightarrow b$)=0,即量$\overrightarrow a+\overrightarrow b$与$\overrightarrow a-\overrightarrow b$垂直.
(2)由已知得($\sqrt{3}\overrightarrow a+\overrightarrow b$)2=($\overrightarrow a-\sqrt{3}\overrightarrow b$)2,
⇒$3{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2\sqrt{3}\overrightarrow{a}•\overrightarrow{b}$=${\overrightarrow{a}}^{2}+3{\overrightarrow{b}}^{2}-2\sqrt{3}\overrightarrow{a}•\overrightarrow{b}$,即$\frac{\sqrt{3}}{2}sinα-\frac{1}{2}cosα=sin(α-\frac{π}{6})=0$.可求得α
解答 解:(1)证明:∵向量$\overrightarrow a=(cosα,sinα)(0≤α<2π),\overrightarrow b=(-\frac{1}{2},\frac{{\sqrt{3}}}{2}),\overrightarrow a$与$\overrightarrow b$不共线.
∴|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,则得($\overrightarrow a+\overrightarrow b$)•($\overrightarrow a-\overrightarrow b$)=${\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}={1}^{2}-{1}^{2}=0$,
∴$\overrightarrow a+\overrightarrow b$与$\overrightarrow a-\overrightarrow b$垂直.
(2)∵向量$\sqrt{3}\overrightarrow a+\overrightarrow b$与$\overrightarrow a-\sqrt{3}\overrightarrow b$的模相等,
∴($\sqrt{3}\overrightarrow a+\overrightarrow b$)2=($\overrightarrow a-\sqrt{3}\overrightarrow b$)2,
⇒$3{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2\sqrt{3}\overrightarrow{a}•\overrightarrow{b}$=${\overrightarrow{a}}^{2}+3{\overrightarrow{b}}^{2}-2\sqrt{3}\overrightarrow{a}•\overrightarrow{b}$,
∵${\overrightarrow{a}}^{2}={\overrightarrow{b}}^{2}$,∴$\overrightarrow{a}•\overrightarrow{b}=0$
∴$\frac{\sqrt{3}}{2}sinα-\frac{1}{2}cosα=sin(α-\frac{π}{6})=0$.
∵α∈[0,2π),∴$α=\frac{π}{6}$或$α=\frac{7π}{6}$.
点评 本题考查了向量的数量积运算,属于中档题.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
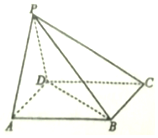 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,且平面PAD⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,且平面PAD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是某年青年歌手大奖赛中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个).去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )
如图是某年青年歌手大奖赛中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个).去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )| A. | a1>a2 | B. | a1<a2 | ||
| C. | a1=a2 | D. | a1,a2的大小与m的值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a•1.1n-nb | B. | a•1.1n-10b(1.1n-1) | ||
| C. | n(1.1a-1) | D. | (a-b)1.1n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com