
分析 (1)由已知可求$\frac{1}{2}=\frac{1}{2}cos({2×\frac{π}{6}-φ})$,结合范围0<φ<π,即可得解φ的值;
(2)由(1)利用三角函数平移变换的规律可求$y=g(x)=\frac{1}{2}cos({4x-\frac{π}{3}})$,由$x∈[{0,\frac{π}{4}}]$,利用余弦函数的图象可求其值域.
解答 解:(1)∵$f(x)=\frac{1}{2}cos({2x-φ})$,且函数图象过点$({\frac{π}{6},\frac{1}{2}})$,
∴$\frac{1}{2}=\frac{1}{2}cos({2×\frac{π}{6}-φ})$,即$cos({\frac{π}{3}-φ})=1$,解得$φ=\frac{π}{3}+2kπ,k∈{z}$.
又0<φ<π,
∴$φ=\frac{π}{3}$.
(2)由(1)知$f(x)=\frac{1}{2}cos({2x-\frac{π}{3}})$,
将函数y=f(x)的图象上各点的横坐标缩短到原来的$\frac{1}{2}$,
纵坐标不变,得到函数$y=g(x)=\frac{1}{2}cos({4x-\frac{π}{3}})$的图象.
∵$x∈[{0,\frac{π}{4}}]$,
∴$4x-\frac{π}{3}∈[{-\frac{π}{3},\frac{2π}{3}}]$,
故$-\frac{1}{2}≤cos({4x-\frac{π}{3}})≤1$.
∴y=g(x)在$[{0,\frac{π}{4}}]$上的最大值和最小值分别为$\frac{1}{2}$和$-\frac{1}{4}$.
点评 本题主要考查了三角函数平移变换的规律,余弦函数的图象和性质,三角函数恒等变换的应用,考查了计算能力和数形结合思想,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | (4,16) | B. | (0,12) | C. | (9,21) | D. | (14,16) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,3) | B. | $(-∞,2\sqrt{2})$ | C. | (-∞,$\frac{11}{3}$) | D. | (-∞,$\frac{9}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
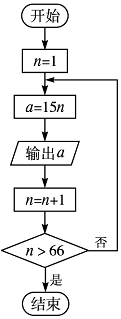
| A. | 输出不大于990且能被15整除的所有正整数 | |
| B. | 输出不大于66且能被15整除的所有正整数 | |
| C. | 输出67 | |
| D. | 输出能被15整除且大于66的正整数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
| 场数 | 9 | 10 | 11 | 12 | 13 | 14 |
| 人数 | 10 | 18 | 22 | 25 | 20 | 5 |
| 非歌迷 | 歌迷 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com