
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
| 场数 | 9 | 10 | 11 | 12 | 13 | 14 |
| 人数 | 10 | 18 | 22 | 25 | 20 | 5 |
| 非歌迷 | 歌迷 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 |
分析 (1)由统计表可知,在抽取的100人中,“歌迷”有25人,完成2×2列联表,求出k2的观测值k2=$\frac{100}{33}$≈3.030<3.841,由此得到我们不能在犯错误的概率不超过0.05的前提下认为“歌迷”与性别有关.
(2)由统计表可知,“超级歌迷”有5人,利用列举法能求出至少有1名女性观众的概率.
解答 解:(1)由统计表可知,在抽取的100人中,“歌迷”有25人,
从而完成2×2列联表如下:
| 非歌迷 | 歌迷 | 总计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 总计 | 75 | 25 | 100 |
点评 本题考查独立检验的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤-1} | B. | {x|x≥3} | C. | $\{x|x<-\frac{5}{4}\}$ | D. | $\{x|-\frac{5}{4}≤x<-1\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,一个正六角星薄片(其对称轴与水平面垂直)匀速地升长水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(x)的图象大致为( )
如图,一个正六角星薄片(其对称轴与水平面垂直)匀速地升长水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(x)的图象大致为( )| A. | 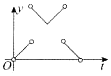 | B. | 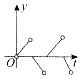 | C. | 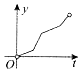 | D. | 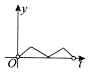 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com