
| A�� | ��4��16�� | B�� | ��0��12�� | C�� | ��9��21�� | D�� | ��14��16�� |
���� ��������f��x����ͼ��ȷ��x1x2=1��x3+x4=12��2��x3��4��8��x4��10���ɴ˿ɵ�$\frac{{2{x_3}+{x_4}}}{{{x_1}{x_2}}}$��ȡֵ��Χ��
��� �⣺������ͼ����ͼ��ʾ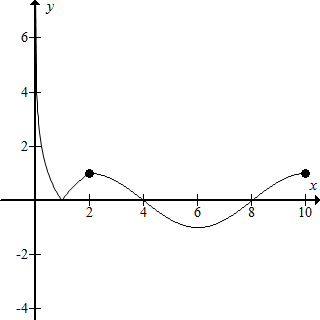
����0��x1��1��x2��2��x3��x4����x3��x4����x=6�Գƣ�
��f��x1��=f��x2����
��-log2x1=log2x2��
��log2x1x2=0��
��x1x2=1��
��f��x3��=f��x4����
��x3+x4=12��2��x3��4��8��x4��10��
��$\frac{{2{x_3}+{x_4}}}{{{x_1}{x_2}}}$=2x3+x4=x3+12��
��$\frac{{2{x_3}+{x_4}}}{{{x_1}{x_2}}}$��ȡֵ��ΧΪ��14��16��
��ѡD��
���� ���⿼��ֶκ�����ͼ����������ֵ���Ӧ�á������뷽�̵��ۺ�Ӧ�õȻ���֪ʶ����������������������ν��������������ת��˼�룬�ѶȽϴ�


 ��ս100��Ԫ����Ծ�ϵ�д�
��ս100��Ԫ����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -14 | B�� | -28 | C�� | 14 | D�� | 28 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
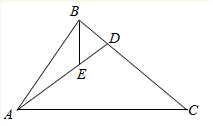 ��ͼ���ڡ�ABC�У���֪��BAC=$\frac{��}{3}$��|$\overrightarrow{AB}$|=2��|$\overrightarrow{AC}$|=3����DΪ��BC��һ�㣬����$\overrightarrow{AC}$+2$\overrightarrow{AB}$=3$\overrightarrow{AD}$����E��AD��һ�㣬����$\overrightarrow{AE}$=2$\overrightarrow{ED}$����|$\overrightarrow{BE}$|=$\frac{2\sqrt{19}}{9}$��
��ͼ���ڡ�ABC�У���֪��BAC=$\frac{��}{3}$��|$\overrightarrow{AB}$|=2��|$\overrightarrow{AC}$|=3����DΪ��BC��һ�㣬����$\overrightarrow{AC}$+2$\overrightarrow{AB}$=3$\overrightarrow{AD}$����E��AD��һ�㣬����$\overrightarrow{AE}$=2$\overrightarrow{ED}$����|$\overrightarrow{BE}$|=$\frac{2\sqrt{19}}{9}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
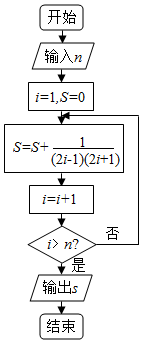
| A�� | $\frac{4}{9}$ | B�� | $\frac{8}{9}$ | C�� | $\frac{5}{11}$ | D�� | $\frac{10}{11}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com