
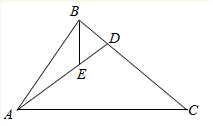
 如图,在△ABC中,已知∠BAC=$\frac{π}{3}$,|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=3,点D为边BC上一点,满足$\overrightarrow{AC}$+2$\overrightarrow{AB}$=3$\overrightarrow{AD}$,点E是AD上一点,满足$\overrightarrow{AE}$=2$\overrightarrow{ED}$,则|$\overrightarrow{BE}$|=$\frac{2\sqrt{19}}{9}$.
如图,在△ABC中,已知∠BAC=$\frac{π}{3}$,|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=3,点D为边BC上一点,满足$\overrightarrow{AC}$+2$\overrightarrow{AB}$=3$\overrightarrow{AD}$,点E是AD上一点,满足$\overrightarrow{AE}$=2$\overrightarrow{ED}$,则|$\overrightarrow{BE}$|=$\frac{2\sqrt{19}}{9}$. 分析 用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{BE}$,计算${\overrightarrow{BE}}^{2}$即可得出|$\overrightarrow{BE}$|.
解答 解:如图,延长AB到F,使AF=2AB,连接CF,
取CF中点O,连接AO,则$\overrightarrow{AC}$+2$\overrightarrow{AB}$=2$\overrightarrow{AO}$=3$\overrightarrow{AD}$,
∴$\overrightarrow{AD}=\frac{2}{3}\overrightarrow{AO}$,$\overrightarrow{AO}$=$\frac{1}{2}$($\overrightarrow{AC}+2\overrightarrow{AB}$),
∵$\overrightarrow{AE}$=2$\overrightarrow{ED}$,
∴$\overrightarrow{AE}=\frac{2}{3}\overrightarrow{AD}=\frac{4}{9}\overrightarrow{AO}$=$\frac{2}{9}$($\overrightarrow{AC}+2\overrightarrow{AB}$)=$\frac{4}{9}\overrightarrow{AB}+\frac{2}{9}\overrightarrow{AC}$;
∵∠BAC=$\frac{π}{3}$,∴$\overrightarrow{AB}•\overrightarrow{AC}$=2×3×cos60°=3,
∴$\overrightarrow{BE}$=$\overrightarrow{BA}+\overrightarrow{AE}$=-$\frac{5}{9}\overrightarrow{AB}$+$\frac{2}{9}$$\overrightarrow{AC}$,
∴${\overrightarrow{BE}}^{2}$=(-$\frac{5}{9}\overrightarrow{AB}$+$\frac{2}{9}$$\overrightarrow{AC}$)2=$\frac{25}{81}$${\overrightarrow{AB}}^{2}$+$\frac{4}{81}{\overrightarrow{AC}}^{2}$-$\frac{20}{81}$$\overrightarrow{AB}•\overrightarrow{AC}$=$\frac{76}{81}$,
∴|$\overrightarrow{BE}$|=$\sqrt{\frac{76}{81}}$=$\frac{2\sqrt{19}}{9}$.
故答案为:$\frac{2\sqrt{19}}{9}$.
点评 本题考查了平面向量的数量积运算,平面向量的几何运算,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,16) | B. | (0,12) | C. | (9,21) | D. | (14,16) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com