
分析 作差,分解,利用实数的性质,可得:($\frac{a}{\sqrt{b}}$+$\frac{b}{\sqrt{a}}$)-($\sqrt{a}$+$\sqrt{b}$)=$\frac{(\sqrt{a}-\sqrt{b})^{2}(\sqrt{a}+\sqrt{b})}{\sqrt{ab}}$>0.进而得到结论.
解答 解:($\frac{a}{\sqrt{b}}$+$\frac{b}{\sqrt{a}}$)-($\sqrt{a}$+$\sqrt{b}$)
=$\frac{a-b}{\sqrt{b}}$-$\frac{a-b}{\sqrt{a}}$
=(a-b)$\frac{\sqrt{a}-\sqrt{b}}{\sqrt{ab}}$
=$\frac{(\sqrt{a}-\sqrt{b})^{2}(\sqrt{a}+\sqrt{b})}{\sqrt{ab}}$>0.
故$\frac{a}{\sqrt{b}}$+$\frac{b}{\sqrt{a}}$>$\sqrt{a}$+$\sqrt{b}$,
故答案为:$\frac{a}{\sqrt{b}}$+$\frac{b}{\sqrt{a}}$>$\sqrt{a}$+$\sqrt{b}$
点评 本题考查的知识点是作差法比较数的大小,不等式的证明,难度中档.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | 1 | D. | $\sqrt{3}+\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -14 | B. | -28 | C. | 14 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{33}{36}$ | B. | $\frac{3}{4}$ | C. | $\frac{9}{11}$ | D. | $\frac{5}{18}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
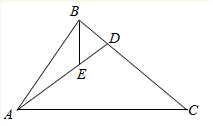 如图,在△ABC中,已知∠BAC=$\frac{π}{3}$,|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=3,点D为边BC上一点,满足$\overrightarrow{AC}$+2$\overrightarrow{AB}$=3$\overrightarrow{AD}$,点E是AD上一点,满足$\overrightarrow{AE}$=2$\overrightarrow{ED}$,则|$\overrightarrow{BE}$|=$\frac{2\sqrt{19}}{9}$.
如图,在△ABC中,已知∠BAC=$\frac{π}{3}$,|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=3,点D为边BC上一点,满足$\overrightarrow{AC}$+2$\overrightarrow{AB}$=3$\overrightarrow{AD}$,点E是AD上一点,满足$\overrightarrow{AE}$=2$\overrightarrow{ED}$,则|$\overrightarrow{BE}$|=$\frac{2\sqrt{19}}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
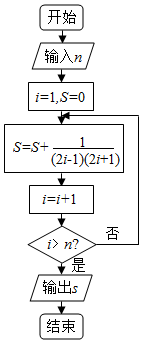
| A. | $\frac{4}{9}$ | B. | $\frac{8}{9}$ | C. | $\frac{5}{11}$ | D. | $\frac{10}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com