
分析 根据题意,令f1(x)=a1=f(x)=$\frac{{x}^{2}}{2x+1}$,则有f2(x)=a2=f[f1(x)]=$\frac{{{a}_{1}}^{2}}{{2a}_{1}+1}$,依次可得fn+1(x)=an+1=f[fn(x)]=$\frac{{{a}_{n}}^{2}}{{2a}_{n}+1}$,分析可得即有$\frac{1}{{a}_{n+1}}$+1=$\frac{1}{{{a}_{n}}^{2}}$+$\frac{2}{{a}_{n}}$+1=($\frac{1}{{a}_{n}}$+1)2,由等比数列的性质分析可得lg($\frac{1}{{a}_{n}}$+1)是首项为lg($\frac{1}{{a}_{1}}$+1),公比为2的等比数列;进而可以求出数列{an}的通项公式,将n=10代入可得a10=f10(x)的解析式,再将x=$\frac{1}{2}$代入计算可得答案.
解答 解:∵f(x)=$\frac{{x}^{2}}{2x+1}$,f1(x)=f(x),fn(x)=$\underset{\underbrace{f(…f(x)…)}}{n个f}$,
令f1(x)=a1=f(x)=$\frac{{x}^{2}}{2x+1}$,
f2(x)=a2=f[f1(x)]=$\frac{{{a}_{1}}^{2}}{{2a}_{1}+1}$,
…
fn+1(x)=an+1=f[fn(x)]=$\frac{{{a}_{n}}^{2}}{{2a}_{n}+1}$,
即有an+1=$\frac{{{a}_{n}}^{2}}{{2a}_{n}+1}$,
变形可得:$\frac{1}{{a}_{n+1}}$=$\frac{1}{{{a}_{n}}^{2}}$+$\frac{2}{{a}_{n}}$,
$\frac{1}{{a}_{n+1}}$+1=$\frac{1}{{{a}_{n}}^{2}}$+$\frac{2}{{a}_{n}}$+1=($\frac{1}{{a}_{n}}$+1)2,
lg($\frac{1}{{a}_{n+1}}$+1)=lg[($\frac{1}{{a}_{n}}$+1)2]=2lg($\frac{1}{{a}_{n}}$+1),
故lg($\frac{1}{{a}_{n}}$+1)是首项为lg($\frac{1}{{a}_{1}}$+1),公比为2的等比数列;
则有lg($\frac{1}{{a}_{n}}$+1)=lg($\frac{1}{{a}_{1}}$+1)×2n-1,
$\frac{1}{{a}_{n}}$+1=($\frac{1}{{a}_{1}}$+1)${\;}^{{2}^{n-1}}$,
当n=10时,有$\frac{1}{{a}_{10}}$+1=($\frac{1}{{a}_{1}}$+1)${\;}^{{2}^{9}}$,
又由a1=$\frac{{x}^{2}}{2x+1}$,则$\frac{1}{{a}_{1}}$+1=($\frac{x+1}{x}$)2,
a10=f10(x)=$\frac{1}{(\frac{x+1}{x})^{{2}^{10}}-1}$,
令x=$\frac{1}{2}$,
则${f_{10}}(\frac{1}{2})$=$\frac{1}{{{3^{1024}}-1}}$;
故答案为:$\frac{1}{{{3^{1024}}-1}}$.
点评 本题考查数列的应用,关键是构造等比数列,并运用等比数列的性质分析,求出数列的通项公式.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤-3 | B. | a≤1 | C. | a≥-1 | D. | a≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,3) | B. | $(-∞,2\sqrt{2})$ | C. | (-∞,$\frac{11}{3}$) | D. | (-∞,$\frac{9}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=cos(\frac{1}{4}x-\frac{π}{4})$ | B. | y=-sinx | C. | y=-cosx | D. | $y=sin(x+\frac{π}{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
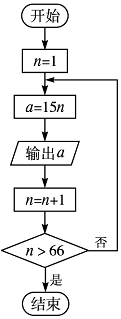
| A. | 输出不大于990且能被15整除的所有正整数 | |
| B. | 输出不大于66且能被15整除的所有正整数 | |
| C. | 输出67 | |
| D. | 输出能被15整除且大于66的正整数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (1,+∞) | C. | (0,2) | D. | (2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com