
| A. | (-∞,3) | B. | $(-∞,2\sqrt{2})$ | C. | (-∞,$\frac{11}{3}$) | D. | (-∞,$\frac{9}{2}$) |
分析 求出¬p成立时,?x∈[2,4],都有a≥x+$\frac{2}{x}$恒成立,从而求出p为真时,a的范围即可.
解答 解:命题P:至少存在一个实数x0∈[2,4],使不等式x2-ax+2>0成立,
则¬p:?x∈[2,4],都有x2-ax+2≤0成立,
即?x∈[2,4],都有a≥x+$\frac{2}{x}$恒成立,
令f(x)=x+$\frac{2}{x}$,x∈[2,4],
则f′(x)=1-$\frac{2}{{x}^{2}}$=$\frac{{x}^{2}-2}{{x}^{2}}$>0,
故f(x)在[2,4]递增,
f(x)max=f(4)=4+$\frac{1}{2}$=$\frac{9}{2}$,
故a≥$\frac{9}{2}$,
即¬p成立时,a≥$\frac{9}{2}$,
故p为真时,a<$\frac{9}{2}$,
故选:D.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,考查命题的否定,是一道中档题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:选择题
| A. | -14 | B. | -28 | C. | 14 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
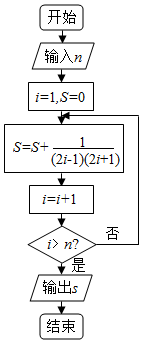
| A. | $\frac{4}{9}$ | B. | $\frac{8}{9}$ | C. | $\frac{5}{11}$ | D. | $\frac{10}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | 11 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤-1} | B. | {x|x≥3} | C. | $\{x|x<-\frac{5}{4}\}$ | D. | $\{x|-\frac{5}{4}≤x<-1\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com