
分析 没有限制条件的排列有A88=40320种,其中甲、乙同排的有C21C62A44A44=17280种,故(1),(2),(5)问题得以解决;
(3)分两类,甲、乙同排相邻,和甲乙前后相邻,根据分类计数原理可得,
(4)选从中间4个位置选2个排甲乙,其余的人任意排,问题得以解决.
解答 解:(1)没有限制条件的排列有A88=40320种,其中甲、乙同排的有C21C62A44A44=17280种,
故甲、乙不同排有40320-17280=23040种,
(2)由(1)可得甲、乙同排有C21C62A44A44=17280种,
(3)甲、乙同排相邻,把甲乙捆绑在一起,看做一个复合元素,从相邻的6个位置选一个,其余的任意排,故有A22A61A66=8640种,
甲乙前后相邻,从4个位置选一个,其余的任意排,故有A22A41A66=5760种,
根据分类计数原理,共有8640+5760=14400种.
(4)选从中间4个位置选2个排甲乙,其余的人任意排,故有A42A66=17280种
(5)没有限制条件的排列有A88=40320种
点评 本题考查分步分类计数原理,考查学生的计算能力分析问题的能力,属于中档题.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | -9 | B. | -1 | C. | 1 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
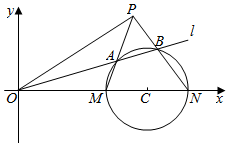 在平面直角坐标系xOy中,圆C的方程为(x-4)2+y2=1,且圆C与x轴交于M,N两点,设直线l的方程为y=kx(k>0)
在平面直角坐标系xOy中,圆C的方程为(x-4)2+y2=1,且圆C与x轴交于M,N两点,设直线l的方程为y=kx(k>0)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com