
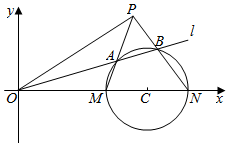
 ��ƽ��ֱ������ϵxOy�У�ԲC�ķ���Ϊ��x-4��2+y2=1����ԲC��x�ύ��M��N���㣬��ֱ��l�ķ���Ϊy=kx��k��0��
��ƽ��ֱ������ϵxOy�У�ԲC�ķ���Ϊ��x-4��2+y2=1����ԲC��x�ύ��M��N���㣬��ֱ��l�ķ���Ϊy=kx��k��0������ ��1��������k��0��Բ��C��ֱ��l�ľ���d=$\frac{4k}{\sqrt{1+{k}^{2}}}$����ֱ��l��ԲC���е�k=$\frac{\sqrt{15}}{15}$���ɴ������ֱ��l��
��2����i���������0��AB=2$\sqrt{1-{d}^{2}}$��$\frac{2\sqrt{17}}{17}$���Ӷ�d=$\frac{4k}{\sqrt{1+{k}^{2}}}$���ɴ������ʵ��k��ȡֵ��Χ��
��ii��lAM��y=k1��x-3������ԲC����x-4��2+y2=1��������$��x-3��[��1+{{k}_{1}}^{2}��x-��3{{k}_{1}}^{2}+5��]=0$����Τ�ﶨ�����A��B�����꣬�Ӷ��õ���1+k1k2����3k1+5k2��=0���ɴ���֤�����ڳ���a=2��ʹ��k1+k2=2k3�������
��� �⣺��1��������k��0��
��Բ��C��ֱ��l�ľ���d=$\frac{4k}{\sqrt{1+{k}^{2}}}$��
��ֱ��l��ԲC���У�
��d=$\frac{4k}{\sqrt{1+{k}^{2}}}$=1�����k=$\frac{\sqrt{15}}{15}$��
��ֱ��l��y=$\frac{\sqrt{15}}{15}$x��
��2����i���������0��AB=2$\sqrt{1-{d}^{2}}$��$\frac{2\sqrt{17}}{17}$��
���$\frac{4\sqrt{17}}{17}��d��1$��
�ɣ�1��֪d=$\frac{4k}{\sqrt{1+{k}^{2}}}$��
��$\frac{4\sqrt{17}}{17}��\frac{4k}{\sqrt{1+{k}^{2}}}��1$��
��$\frac{1}{4}��k��\frac{\sqrt{15}}{15}$��
��ii��lAM��y=k1��x-3����
��ԲC����x-4��2+y2=1������
��$��x-3��[��1+{{k}_{1}}^{2}��x-��3{{k}_{1}}^{2}+5��]=0$��
��${x}_{M}=3��{x}_{A}=\frac{3{{k}_{1}}^{2}+5}{1+{{k}_{1}}^{2}}$��
��A��$\frac{3{{k}_{1}}^{2}+5}{1+{{k}_{1}}^{2}}$��$\frac{2{k}_{1}}{1+{{k}_{1}}^{2}}$����
ͬ������B��$\frac{5{{k}_{2}}^{2}+3}{1+{{k}_{2}}^{2}}$��$\frac{-2{k}_{2}}{1+{{k}_{2}}^{2}}$����
��kOA=kOB��
��$\frac{\frac{2{k}_{1}}{1+{{k}_{1}}^{2}}}{\frac{3{{k}_{1}}^{2}+5}{1+{{k}_{1}}^{2}}}$=$\frac{\frac{-2{k}_{2}}{1+{{k}_{2}}^{2}}}{\frac{5{{k}_{2}}^{2}+3}{1+{{k}_{2}}^{2}}}$������1+k1k2����3k1+5k2��=0��
��k1k2��-1��
��${k}_{2}=-\frac{3}{5}{k}_{1}$��
��P��x0��y0����
��$\left\{\begin{array}{l}{{y}_{0}={k}_{1}��{x}_{0}-3��}\\{{y}_{0}={k}_{2}��{x}_{0}-5��}\end{array}\right.$��
��$\left\{\begin{array}{l}{{x}_{0}=\frac{3{k}_{1}-5{k}_{2}}{{k}_{1}-{k}_{2}}}\\{{y}_{0}=\frac{-2{k}_{1}{k}_{2}}{{k}_{1}-{k}_{2}}}\end{array}\right.$��
��P��$\frac{3{k}_{1}-5{k}_{2}}{{k}_{1}-{k}_{2}}$��$\frac{-2{k}_{1}{k}_{2}}{{k}_{1}-{k}_{2}}$������P��$\frac{15}{4}$��$\frac{3{k}_{1}}{4}$����
��${k}_{3}=\frac{\frac{3{k}_{1}}{4}}{\frac{15}{4}}$=$\frac{{k}_{1}}{5}$��
��${k}_{1}+{k}_{2}=\frac{2}{5}{k}_{1}=2{k}_{3}$��
����ڳ���a=2��ʹ��k1+k2=2k3�������
���� ���⿼��ֱ�߷��̵�������ֱ�ߵ�б�ʵ�ȡֵ��Χ���������Ƿ����ʹ�õ�ʽ������ij������ж���֤�������е��⣬����ʱҪ�������⣬ע��Բ�����ʵĺ������ã�


 ȫ�ܲ��һ���þ�ϵ�д�
ȫ�ܲ��һ���þ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6�� | B�� | 12�� | C�� | 8�� | D�� | 16�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��x��=3x3+2x2+1 | B�� | f��x��=${x^{-\frac{1}{2}}}$ | C�� | f��x��=3x | D�� | f��x��=$\frac{{\sqrt{4-{x^2}}}}{{|{x+3}|-3}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��������� | B�� | �۽������� | ||
| C�� | ����ֱ�������� | D�� | ������ֱ�������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ijѧУ�����꼶��800�������������ȡ50�˲������ߣ����ݱ���������ѧ������ȫ������155cm��195cm֮�䣬��������������·�ʽ�ֳɰ��飺��һ��[155��160�����ڶ���[160��165���������ڰ���[190��195]����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣���֪��һ����ڰ���������ͬ��������ȵ�������1�ˣ�
��ijѧУ�����꼶��800�������������ȡ50�˲������ߣ����ݱ���������ѧ������ȫ������155cm��195cm֮�䣬��������������·�ʽ�ֳɰ��飺��һ��[155��160�����ڶ���[160��165���������ڰ���[190��195]����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣���֪��һ����ڰ���������ͬ��������ȵ�������1�ˣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com