
分析 设最大限制时速为x千米/时.汽车在离开障碍物40-5=35(米)处,必须停下,建立方程,即可得出结论.
解答 解:设最大限制时速为x千米/时,汽车在离开障碍物40-5=35(米)处,必须停下.
另外,1.5秒钟内,汽车行驶的距离是:1.5×$\frac{1}{3600}$×x×1000=$\frac{5}{12}$x(米),
因此,$\frac{5}{12}$x+=$\frac{1}{60}$x2=35,
所以x2+25x-35×60=0,
所以(x+60)(x-35)=0,于是得到x=35,
即最大限制时速为35千米/时.
点评 本题考查利用数学知识解决实际问题,考查学生的计算能力,注意单位的统一.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
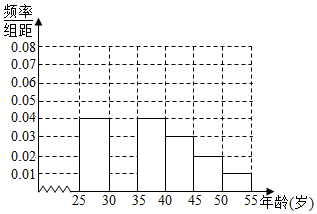 某校学生利用元旦节进行社会实践,在[25,55]岁的人群随机抽取n人,进行了一次“是否已养成垃圾分类习惯”的调查,得到如下统计表和各年龄段人数频率分布直方图:
某校学生利用元旦节进行社会实践,在[25,55]岁的人群随机抽取n人,进行了一次“是否已养成垃圾分类习惯”的调查,得到如下统计表和各年龄段人数频率分布直方图:| 组数 | 分组 | 已养成垃圾分类习惯的人数 | 占本组频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六祖 | [50,55] | 15 | 0.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com