Question

8．已知函数F（x）=sinx•f′（x）是定义在R上的偶函数，且当x≥0时，f（x）=2a|x-1|-a，其中a＞0为常数．若函数y=f[f（x）]有10个零点，则a的取值范围是$（\frac{1}{2}，\frac{3}{2}）$．

Answer 1

分析 利用函数是偶函数，通过x＞0求出f（x）的零点，画出函数的图象，判断x＞0时由5个零点，推出结果即可．

解答 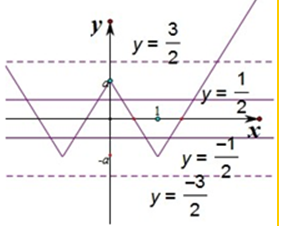解：当x≥0时，f（x）=2a|x-1|-a=a（2|x-1|-1）=0，可得2|x-1|-1=0，解得x=$\frac{1}{2}$或x=$\frac{3}{2}$，
∵f（x）是偶函数，∴当x＜0时，f（x）=0的另外两个解为：$-\frac{1}{2}$和$-\frac{3}{2}$，由选项可得a＞0，
作出函数的图象如图：
设t=f（x），则有y=f（f（x））=0得，f（t）=0，
可得t=$±\frac{1}{2}$或$±\frac{3}{2}$，
∵f（x）是偶函数，
∴要使函数y=f（f（x））恰有10个零点，
则等价于x＞0时，y=f（f（x））恰有5个零点，有函数的图象可得：$\left\{\begin{array}{l}{\frac{1}{2}＜a}\\{\frac{3}{2}＞a}\end{array}\right.$，即$\frac{1}{2}＜a＜\frac{3}{2}$．
故答案为：$（\frac{1}{2}，\frac{3}{2}）$．

点评 本题考查函数的单调性，考查函数的零点，考查函数的周期性与奇偶性，利用数形结合的思想来求解，会化难为易．