
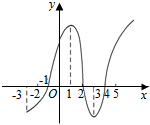
 如图所示是y=f(x)的导数图象,则正确的判断是( )
如图所示是y=f(x)的导数图象,则正确的判断是( )| A. | ①②③ | B. | ②③ | C. | ③④ | D. | ①③④ |
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 20 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21种 | B. | 33种 | C. | 34种 | D. | 40种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对于任意的x∈R,x2+1≤0 | B. | 存在x∈R,x2+1≤0 | ||
| C. | 存在x∈R,x2+1<0 | D. | 存在x∈R,x2+1>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 把a(b+c)与 loga(x+y)类比,则有:loga(x+y)=logax+logay | |
| B. | 把a(b+c)与 sin(x+y)类比,则有:sin(x+y)=sinx+siny | |
| C. | 把(ab)n与 (a+b)n类比,则有:(x+y)n=xn+yn. | |
| D. | 把(a+b)+c与 (xy)z类比,则有:(xy)z=x(yz) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
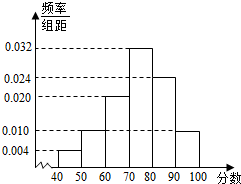 某校从高一年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
某校从高一年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)>c>f(-1) | B. | f(1)<c<f(-1) | C. | f(1)>f(-1)>c | D. | f(1)<f(-1)<c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com