
分析 (1)利用直线上两点以及直线倾斜角表示直线斜率,得到关于θ的等式,求出tanθ.
(2)由题意知,直线l的斜率必存在,且不为零,则设l:y-4=k(x-3),由直线l与两坐标轴围成等腰直角三角形,由此得到直线在x,y轴上的截距的绝对值相等,得到关于斜率k的方程求出斜率.
解答 解:(1)直线l的斜率为k=tanθ=$\frac{4-sinθ}{3-cosθ}$,…(2分)
解得4cosθ=3sinθ,即tan$θ=\frac{4}{3}$…(4分)
所以直线l的斜率为$\frac{4}{3}$,直线l的方程为y=$\frac{4}{3}x$;…(6分)
(2)由题意知,直线l的斜率必存在,且不为零,则设l:y-4=k(x-3),…(7分)
分别令x,y等于零得到x轴上的截距为$-\frac{4}{k}+3$,y轴上的截距为-3k+4,…(8分)
由|$-\frac{4}{k}$+3|=|-3k+4|,
得-$\frac{4}{k}$+3=-3k+4,解得k=-1,或k=$\frac{4}{3}$;…(10分)
或者-$\frac{4}{k}$+3=3k-4,解得k=1或k=$\frac{4}{3}$;…(12分)
经检验k=$\frac{4}{3}$不合题意,舍去.…(13分)
综上:k的值为±1,直线l的方程为:y=x+1或y=-x+7.…(14分).
点评 本题考查了直线的斜率以及直线在坐标轴上的截距.考查了讨论的思想.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:解答题
 海上某货轮在A处看灯塔B在货轮的北偏东75°,距离为12$\sqrt{6}$海里;在A处看灯塔C在货轮的北偏西30°,距离为8$\sqrt{3}$海里;货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°.
海上某货轮在A处看灯塔B在货轮的北偏东75°,距离为12$\sqrt{6}$海里;在A处看灯塔C在货轮的北偏西30°,距离为8$\sqrt{3}$海里;货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
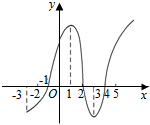 如图所示是y=f(x)的导数图象,则正确的判断是( )
如图所示是y=f(x)的导数图象,则正确的判断是( )| A. | ①②③ | B. | ②③ | C. | ③④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{9}{2}$ | B. | $\frac{9}{2}$ | C. | $\frac{1}{4}$ | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
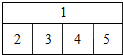 用4种不同的颜色填涂如图所示的1,2,3,4,5五个区域,要求一区一色,邻区异色,则不同的填涂方法种数是( )
用4种不同的颜色填涂如图所示的1,2,3,4,5五个区域,要求一区一色,邻区异色,则不同的填涂方法种数是( )| A. | 120 | B. | 96 | C. | 72 | D. | 48 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com