练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．z1=1-2i，z2=3+4i，z3=2+i，$w={z_1}^2$+$\overline{z_2}-\frac{i}{z_3}$，求复数w．

    分析 由题意、共轭复数和复数代数形式的加减乘除运算，依次求出${{z}_{1}}^{2}$、$\overline{{z}_{2}}、\frac{i}{{z}_{3}}$，代入w整理出实部和虚部即可．

    解答 解：∵z1=1-2i，z2=3+4i，z3=2+i，
    ∴${z_1}^2=（1-2i{）^2}=-3-4i$，$\overline{z_2}$=3-4i，$\frac{i}{z_3}=\frac{i}{2+i}=\frac{-1+2i}{5}$，…（6分）
    ∴$w={z_1}^2$+$\overline{z_2}-\frac{i}{z_3}$=-3-4i+3-4i-$\frac{-1+2i}{5}$=$\frac{1}{5}-\frac{42}{5}i$．…（12分）

    点评 本题考查共轭复数的定义，复数代数形式的加减乘除运算，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    8．抽查10件产品，设事件A：至少有两件次品，则A的对立事件为至多一件次品．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．命题“对于任意的x∈R，x2+1＞0”的否定是（　　）
    A．对于任意的x∈R，x2+1≤0B．存在x∈R，x2+1≤0
    C．存在x∈R，x2+1＜0D．存在x∈R，x2+1＞0

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

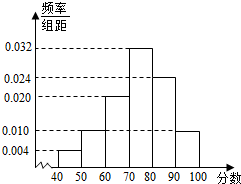    6．某校从高一年级学生中随机抽取50名学生，将他们的期中考试数学成绩（满分100分，成绩均为不低于40分的整数）分成六段：[40，50），[50，60），…，[90，100]，得到如图所示的频率分布直方图．
    （1）若该校高一年级共有学生1000人，试估计成绩不低于60分的人数；
    （2）为了帮助学生提高数学成绩，学校决定在随机抽取的50名学生中成立“二帮一”小组，即从成绩[90，100]中选两位同学，共同帮助[40，50）中的某一位同学．已知甲同学的成绩为42分，乙同学的成绩为95分，求甲、乙恰好被安排在同一小组的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知二次函数f（x）=ax2+bx-3在x=1处取得极值，且在（0，-3）点处的切线与直线2x+y=0平行．
    （1）求f（x）的解析式；
    （2）求函数g（x）=xf（x）+4x的单调递增区间及极值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知直线l：x-ay+3=0的倾斜角为30°，则实数a的值是$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知直线l经过点P（3，4）．
    （1）若直线l的倾斜角为θ（θ≠90°），且直线l经过另外一点（cosθ，sinθ），求此时直线的方程；
    （2）若直线l与两坐标轴围成等腰直角三角形，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．下列有关命题说法正确的是（　　）
    A．命题“若x2=4，则x=2”的否命题为“若x2=4，则x≠2”
    B．所有常数列既是等差数列也是等比数列
    C．命题“若x=y，则sinx=siny”的逆否命题为假命题
    D．命题“?x∈R，x2+x＜0”的否定是“?x∈R，x2+x≥0”．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．（1）计算$\frac{{{{（1+i）}^2}}}{1+2i}+\frac{{{{（1-i）}^2}}}{2-i}$；
    （2）若实数x，y满足$\frac{x}{1+i}+\frac{y}{1+2i}=\frac{10}{1+3i}$，求x，y的值．

    查看答案和解析>>

    同步练习册答案