练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．环卫工人准备在路的一侧依次栽种7棵树，现只有梧桐树和柳树可供选择，则相邻2棵树不同为柳树的栽种方法有（　　）
    A．21种B．33种C．34种D．40种

    分析 分别求出若7颗树没有柳树的方法数、若7颗树中只有1棵、2棵、3棵、4棵柳树的方法数，再把这些方法数相加，即得所求．

    解答 解：由题意可得，柳树可以有0棵，1棵、2棵、3棵、4棵，柳树不能再多了，否则无法满足条件．
    （1）若7棵树全是梧桐树（即柳树有0棵）方法有1种．
    （2）若7棵树中只有1棵柳树，则有7种方法．
    （3）若7棵树中只有有2棵柳树，则把这2棵柳树插入另外5棵梧桐树形成的6个空中，方法有${C}_{6}^{2}$=15种．
    （4）若7棵树中只有3棵柳树，则把这3棵柳树插入另外4棵梧桐树形成的5个空中，方法有${C}_{5}^{3}$=10种．
     （5）若7棵树中有4棵柳树，则把这4棵柳树插入另外3棵梧桐树形成的4个空中，方法有插空${C}_{4}^{4}$=1种．
    故相邻两棵树不同为柳树的栽种方法有 1+7+15+10+1=34种，
    故选：C．

    点评 本题主要考查排列、组合、两个基本原理的应用，体现了分类讨论的数学思想，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    2．已知动点P（x，y）及两定点A（-3，0）和B（3，0），若$\frac{|PA|}{|PB|}$=2，（|PA|、|PB|分别表示点P与点A、B的距离）
    （1）求动点P的轨迹Γ方程．
    （2）动点Q在直线y-x-1=0上，且QM、QN是轨迹Γ的两条切线，M、N是切点，C是轨迹Γ中心，求四边形OMCN面积的最小值及此时直线MN的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．双曲线$\frac{y^2}{12}-\frac{x^2}{4}=1$的顶点到渐近线的距离为$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．海上某货轮在A处看灯塔B在货轮的北偏东75°，距离为12$\sqrt{6}$海里；在A处看灯塔C在货轮的北偏西30°，距离为8$\sqrt{3}$海里；货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°．
    （1）请在方框内用铅笔与直尺画出图形，并标明三个角度的位置和大小；
    （2）A处与D处之间的距离；
    （3）灯塔C与D处之间的距离（用近似值表示，四舍五入，取整数）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．定义为R上的函数f（x）满足f（x）f（x+2）=7，f（1）=3，则f（2015）=$\frac{7}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．从{1，2，3}中随机选取一个数为a，从{1，2，3，4，5}中随机选取一个数为b，则a＞b的概率是（　　）
    A．$\frac{4}{5}$B．$\frac{3}{5}$C．$\frac{2}{5}$D．$\frac{1}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．满足条件|z-i|=|z+3+4i|的复数z在复平面内对应的点的轨迹是（　　）
    A．一条直线B．两条直线C．圆D．椭圆

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

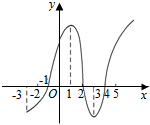    1．如图所示是y=f（x）的导数图象，则正确的判断是（　　）
    ①f（x）在（-3，1）上是增函数；②x=-1是f（x）的极小值点；
    ③f（x）在（2，4）上是减函数，在（-1，2）上是增函数；④x=2是f（x）的极小值点．
    A．①②③B．②③C．③④D．①③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．观察下列式子：1=12，2+3+4=32，3+4+5+6+7=52，4+5+6+7+8+9+10=72，…，可以得出的一般结论是n+（n+1）+（n+2）+…+（n+2n-2）=（2n-1）2．

    查看答案和解析>>

    同步练习册答案