Question

16．某校早上7：30开始上课，假设该校学生小张与小王在早上7：00-7：20之间到校，且每人在该时间段的任何时刻到是等可能的，则小张比小王至少早5分钟到校的概率为多少？

Answer 1

分析 设小张到校的时间为x，小王到校的时间为y．（x，y）可以看成平面中的点试验的全部结果所构成的区域为Ω={（x，y|0≤x≤20，0≤y≤20}是一个矩形区域，则小张比小王至少早5分钟到校事件A={（x，y）|y-x≥5}作出符合题意的图象，由图根据几何概率模型的规则求解即可．

解答 解：设小张到校的时间为x，小王到校的时间为y．
（x，y）可以看成平面中的点试验的全部结果所构成的区域为Ω={（x，y|0≤x≤20，0≤y≤20}是一个矩形区域，对应的面积S=20×20=400，
则小张比小王至少早5分钟到校事件A={x|y-x≥5}作出符合题意的图象，
则符合题意的区域为△ADE，联立$\left\{\begin{array}{l}{y-x=5}\\{y=20}\end{array}\right.$得$\left\{\begin{array}{l}{x=15}\\{y=20}\end{array}\right.$，即D（15，20），
联立$\left\{\begin{array}{l}{y-x=5}\\{x=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=0}\\{y=5}\end{array}\right.$，即E（0，5），
则S_△ADE=$\frac{1}{2}$×15×15，
几何概率模型可知小张比小王至少早5分钟到校的概率为$\frac{\frac{1}{2}×15×15}{20×20}$=$\frac{9}{32}$．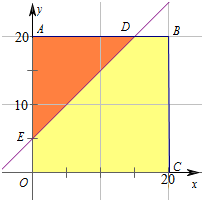

点评 本题考查几何概率模型与模拟方法估计概率，求解的关键是掌握两种求概率的方法的定义及规则，求出对应区域的面积是解决本题的关键．