Question

6．已知菱形ABCD的边长为4，∠ABC=$\frac{5π}{6}$，若在菱形内任取一点，则该点到菱形的四个顶点的距离大于1的概率为1-$\frac{π}{8}$．

Answer 1

分析 根据几何概型的概率公式求出对应区域的面积进行求解即可．

解答 解：分别以A，B，C，D为圆心，1为半径的圆，
则所以概率对应的面积为阴影部分，
则四个圆在菱形内的扇形夹角之和为2π，
则对应的四个扇形之和的面积为一个整圆的面积S=π×1²=π，
∵∠ABC=$\frac{5π}{6}$，
∴∠BAD=$\frac{π}{6}$，
则菱形的面积S=$\frac{1}{2}×4×4×sin\frac{π}{6}×2$=8，
则阴影部分的面积S=8-π，
故所求的概率P=$\frac{8-π}{8}$=1-$\frac{π}{8}$，
故答案为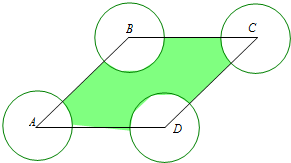：1-$\frac{π}{8}$

点评 本题主要考查几何概型的概率的计算，根据对应分别求出对应区域的面积是解决本题的关键．